题目内容
抛物线y=ax2+bx+
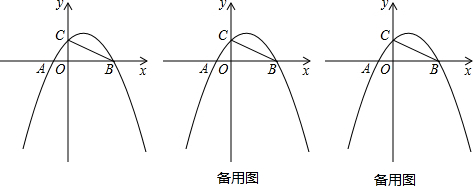
交x轴正半轴于点B及点A(-1,0),交y轴于点C,AB=4.
(1)求抛物线的解析式;
(2)点D在抛物线y=ax2+bx+
在第一象限的部分上(CD与x轴不平行),△BCD的面积为
,求点D的坐标;
(3)在(2)的条件下,点P在抛物线y=ax2+bx+
上,过点P作x轴的垂线,点E为垂足,直线PD交x轴于点F,连接DE,当DE=2DF时,求直线PA与x轴所夹锐角的正切值.
| 3 |
| 2 |
(1)求抛物线的解析式;
(2)点D在抛物线y=ax2+bx+
| 3 |
| 2 |
| 3 |
| 2 |
(3)在(2)的条件下,点P在抛物线y=ax2+bx+
| 3 |
| 2 |

考点:二次函数综合题
专题:
分析:(1)求出A、B坐标,代入函数解析式,列出方程组,求出系数即可;
(2)过点D作y轴的平行线交BC于点G,交x轴于点M,过点C作CH⊥DG,点H为垂足,根据S△BCD=S△CDG+S△DGB求出DG=1,
(3)过点D作PE的垂线,点N为垂足,设点P横坐标t,则P(t,-12t2+t+32),根据当点P位于对称轴右侧时和点P位于对称轴右侧时解答.
(2)过点D作y轴的平行线交BC于点G,交x轴于点M,过点C作CH⊥DG,点H为垂足,根据S△BCD=S△CDG+S△DGB求出DG=1,
(3)过点D作PE的垂线,点N为垂足,设点P横坐标t,则P(t,-12t2+t+32),根据当点P位于对称轴右侧时和点P位于对称轴右侧时解答.
解答:解:(1)∵A(-1,0),
∴OA=1,
∵AB=4,
∴OB=3,
∴B(3,0),
∴
,
解得:
,
∴抛物线的解析式为y=-
x2+x+
.
(2)如图(1),过点C作CH⊥DG,点H为垂足,
设直线BC的解析式为y=mx+n,
∵B(3,0),C(0,
),
∴
,解得
,
∴直线BC的解析式为y=-
x+
.
S△BCD=S△CDG+S△DGB
=
DG•CH+
DG•BM
=
(OM+BM)
=
DG•OB
∵S△BCD=
,OB=3,
∴DG=1,
设点D的横坐标为k,则D(k,-
k2+k+
),G(k,-
k+
),
∴DG=-
k2+k+
-(-
k+
)=1,
∴-
k2+
k=1,
解得k=1或k=2.
当k=1时,D(1,2),当k=2时,D(2,
),则CD∥x轴,舍去;
∴D(1,2).
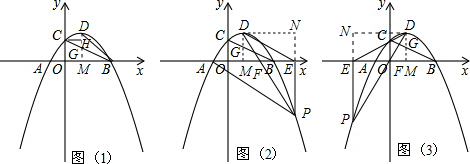
(3)如图(2)、图(3)过点D作y轴的平行线交BC于点G,交x轴于点M,
过点D作PE的垂线,点N为垂足,设点P横坐标t,则P(t,-
t2+t+
),
当点P位于对称轴右侧时,tan∠DPN=
=
=
=
,
tan∠DEM=
,
∴∠DPN=∠DEM,
∴∠MDF=∠DPN=∠DEM,
∵∠DMF=∠EMD,
∴△DMF∽△EMD,
∴
=
,
∵DE=2DF,
∴EM=2DM=4,
∴OE=5,
∴t=5,P(5,-6),
∴tan∠PAE=
=
=1,
当点P位于对称轴左侧时,同理可得:EM=4,OE=3,t=-3,此时P(-3,-6),AE=2,
∴tan∠PAE=
=
=3.
∴OA=1,
∵AB=4,
∴OB=3,
∴B(3,0),
∴
|
解得:
|
∴抛物线的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
(2)如图(1),过点C作CH⊥DG,点H为垂足,
设直线BC的解析式为y=mx+n,
∵B(3,0),C(0,
| 3 |
| 2 |
∴
|
|
∴直线BC的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
S△BCD=S△CDG+S△DGB
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
∵S△BCD=
| 3 |
| 2 |
∴DG=1,
设点D的横坐标为k,则D(k,-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴DG=-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴-
| 1 |
| 2 |
| 3 |
| 2 |
解得k=1或k=2.
当k=1时,D(1,2),当k=2时,D(2,
| 3 |
| 2 |
∴D(1,2).

(3)如图(2)、图(3)过点D作y轴的平行线交BC于点G,交x轴于点M,
过点D作PE的垂线,点N为垂足,设点P横坐标t,则P(t,-
| 1 |
| 2 |
| 3 |
| 2 |
当点P位于对称轴右侧时,tan∠DPN=
| DN |
| PN |
| t-1 | ||||
2-(-
|
| t-1 | ||
|
| 2 |
| t-1 |
tan∠DEM=
| 2 |
| t-1 |
∴∠DPN=∠DEM,
∴∠MDF=∠DPN=∠DEM,
∵∠DMF=∠EMD,
∴△DMF∽△EMD,
∴
| DM |
| EM |
| DF |
| ED |
∵DE=2DF,
∴EM=2DM=4,
∴OE=5,
∴t=5,P(5,-6),
∴tan∠PAE=
| PE |
| EA |
| 6 |
| 6 |
当点P位于对称轴左侧时,同理可得:EM=4,OE=3,t=-3,此时P(-3,-6),AE=2,
∴tan∠PAE=
| PE |
| AE |
| 6 |
| 2 |
点评:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数及二次函数的解析式、锐角三角函数的定义等知识,难度较大.

练习册系列答案
相关题目
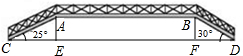 如图是新城市建设中设计的一条人行过街天桥平面设计图,已知桥面AB与地面DC平行,立柱AE⊥CD于点E,立柱BF⊥CD于点F,CD=87.1m,CE=15m,∠ACE=25°,∠BDF=30°
如图是新城市建设中设计的一条人行过街天桥平面设计图,已知桥面AB与地面DC平行,立柱AE⊥CD于点E,立柱BF⊥CD于点F,CD=87.1m,CE=15m,∠ACE=25°,∠BDF=30°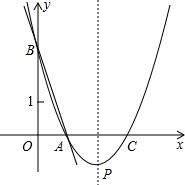 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与X轴交于另一点C,其顶点为P.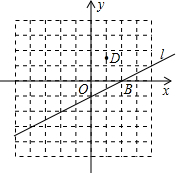 如图,已知直线l的解析式为y=
如图,已知直线l的解析式为y=