题目内容
 如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.
如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.(1)求证:AB与⊙O相切;
(2)若∠AOB=120°,AB=4
| 3 |
考点:切线的判定
专题:数形结合
分析:(1)首先连接OC,然后由OA=OB,C是边AB的中点,根据三线合一的性质,可证得AB与⊙O相切;
(2)首先求得OC的长,继而可求得⊙O的面积.
(2)首先求得OC的长,继而可求得⊙O的面积.
解答: (1)证明:连接OC,
(1)证明:连接OC,
∵在△ABO中,OA=OB,C是边AB的中点,
∴OC⊥AB,
∵以O为圆心的圆过点C,
∴AB与⊙O相切;
(2)解:∵OA=OB,∠AOB=120°,
∴∠A=∠B=30°,
∵AB=4
,C是边AB的中点,
∴AC=
AB=2
,
∴OC=AC•tan∠A=2
×
=2,
∴⊙O的面积为:π×22=4π.
 (1)证明:连接OC,
(1)证明:连接OC,∵在△ABO中,OA=OB,C是边AB的中点,
∴OC⊥AB,
∵以O为圆心的圆过点C,
∴AB与⊙O相切;
(2)解:∵OA=OB,∠AOB=120°,
∴∠A=∠B=30°,
∵AB=4
| 3 |
∴AC=
| 1 |
| 2 |
| 3 |
∴OC=AC•tan∠A=2
| 3 |
| ||
| 3 |
∴⊙O的面积为:π×22=4π.
点评:此题考查了切线的判定、等腰三角形的性质以及三角函数的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
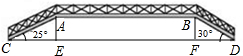 如图是新城市建设中设计的一条人行过街天桥平面设计图,已知桥面AB与地面DC平行,立柱AE⊥CD于点E,立柱BF⊥CD于点F,CD=87.1m,CE=15m,∠ACE=25°,∠BDF=30°
如图是新城市建设中设计的一条人行过街天桥平面设计图,已知桥面AB与地面DC平行,立柱AE⊥CD于点E,立柱BF⊥CD于点F,CD=87.1m,CE=15m,∠ACE=25°,∠BDF=30°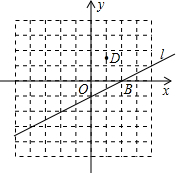 如图,已知直线l的解析式为y=
如图,已知直线l的解析式为y= 实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=
实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y= 如图,形如?ABCD的纸片的对角线AC与BD相交于点O,将这张纸片对折后点B与点D重合,点A落在点E.已知锐角∠AOB=α,那么∠CEO的度数为
如图,形如?ABCD的纸片的对角线AC与BD相交于点O,将这张纸片对折后点B与点D重合,点A落在点E.已知锐角∠AOB=α,那么∠CEO的度数为