题目内容
3.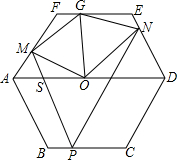 如图,P是正六边形ABCDEF的BC边上的一点,过点P作PM∥AB交AF于M,AD于S,作PN∥CD交DE于N,AD于T,点O是AD的中点,OG平分∠MON,则图中等边三角形有4个.
如图,P是正六边形ABCDEF的BC边上的一点,过点P作PM∥AB交AF于M,AD于S,作PN∥CD交DE于N,AD于T,点O是AD的中点,OG平分∠MON,则图中等边三角形有4个.
分析 连接OE,由△OMA≌△ONE,再证出△GOE≌△NOD,由△ONG是等边三角形和△MOG是等边三角形求出四边形MONG是菱形.,
解答 解:连接OE,如图所示: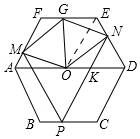 ∵P是正六边形ABCDEF的BC边上的一点,PM∥AB,PN∥CD,
∵P是正六边形ABCDEF的BC边上的一点,PM∥AB,PN∥CD,
∴△AMS、△DNK是等边三角形,
由(2)得,△OMA≌△ONE
∴∠MOA=∠EON,
∵EF∥AO,AF∥OE,
∴四边形AOEF是平行四边形,
∴∠AFE=∠AOE=120°,
∴∠MON=120°,
∴∠GON=60°,
∵∠GOE=60°-∠EON,∠DON=60°-∠EON,
∴∠GOE=∠DON,
∵OD=OE,∠ODN=∠OEG,
在△GOE和△DON中,$\left\{\begin{array}{l}{∠GOE=∠DON}&{\;}\\{OE=OD}&{\;}\\{∠ODN=∠OEG}&{\;}\end{array}\right.$,
∴△GOE≌△NOD(ASA),
∴ON=OG,
又∵∠GON=60°,
∴△ONG是等边三角形,
∴ON=NG,
又∵OM=ON,∠MOG=60°,
∴△MOG是等边三角形,
故答案为:4.
点评 本题主要考查了等边三角形的判定、全等三角形的判定与性质,解题的关键是恰当的作出辅助线,根据三角形全等找出相等的线段.

练习册系列答案
相关题目
14.用四舍五入法按要求对0.64247分别取近似值,其中正确的是( )
| A. | 0.643(精确到百分位) | B. | 0.64(精确到百分位) | ||
| C. | 0.5(精确到0.1) | D. | 0.6424(精确到0.0001) |
8.下列说法正确的是( )
| A. | ab2的次数是2 | B. | 1是单项式 | ||
| C. | $\frac{-3{a}^{3}c}{7}$系数是-3 | D. | 多项式a+b2的次数是3 |
15.某品牌商品,按标价八折出售,仍可获得20%的利润,若该商品标价为18元,则该商品的进价为( )
| A. | 13元 | B. | 12元 | C. | 15元 | D. | 16元 |
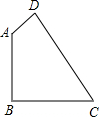 如图,四边形ABCD中,AB=BC=2,AD=1,CD=$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.
如图,四边形ABCD中,AB=BC=2,AD=1,CD=$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.