题目内容
6. 某景区的三个景点A,B,C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.
某景区的三个景点A,B,C在同一线路上,甲、乙两名游客从景点A出发,甲步行到景点C,乙乘景区观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离开景点A后的路程S(米)关于时间t(分钟)的函数图象如图所示.根据以上信息回答下列问题:
(1)乙出发后多长时间与甲相遇?
(2)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?
分析 (1)根据图象确定出甲步行路程与时间的解析式;确定出20≤t≤30时,乙乘观光车由景点A到B时的路程与时间的函数解析式,联立即可确定出相遇的时间;
(2)设当60≤t≤90时,乙步行由景点B到C的速度为x米/分钟,根据题意列出方程,求出方程的解得到x的值,即可确定出乙步行由B到C的速度.
解答 解:(1)当0≤t≤90时,甲步行路程与时间的函数解析式为S=60t;
当20≤t≤30时,设乙乘观光车由景点A到B时的路程与时间的函数解析式为S=mt+n,
把(20,0)与(20,3000)代入得:$\left\{\begin{array}{l}{20m+n=0}\\{30m+n=3000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=300}\\{n=-6000}\end{array}\right.$,
∴函数解析式为S=300t-6000(20≤t≤30);
联立得:$\left\{\begin{array}{l}{S=60t}\\{S=300t-6000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{t=25}\\{S=1500}\end{array}\right.$,
∵25-20=5,
∴乙出发5分钟后与甲相遇;
由60t=3000,得到t=50,即50-25=25,
则乙出发5分钟或25分钟后与甲相遇;
(2)设当60≤t≤90时,乙步行由景点B到C的速度为x米/分钟,
根据题意,得5400-3000-(90-60)x=360,
解得:x=68,
∴乙步行由B到C的速度为68米/分钟.
点评 此题考查了一次函数的应用,弄清图形中表示的意义是解本题的关键.

练习册系列答案
相关题目
19.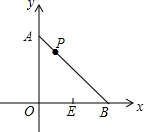 如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2),(2,0),E为OB的中点,P是线段AB上的一个动点,则PE+PO的最小值为( )
如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2),(2,0),E为OB的中点,P是线段AB上的一个动点,则PE+PO的最小值为( )
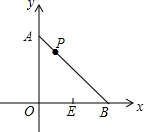 如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2),(2,0),E为OB的中点,P是线段AB上的一个动点,则PE+PO的最小值为( )
如图,在平面直角坐标系中,A、B两点的坐标分别为(0,2),(2,0),E为OB的中点,P是线段AB上的一个动点,则PE+PO的最小值为( )| A. | 2$\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{6}$ |
18.等腰三角形三边长分别为a、b、4,且a、b是关于x的一元二次方程x2-12x+k+2=0的两根,则k的值为( )
| A. | 30 | B. | 34或30 | C. | 36或30 | D. | 34 |


 如图,一次函数y=-$\frac{4}{5}$x+12与x轴、y轴相交于点A、B两点,动点P以4个单位/秒的速度从点O出发,沿OA方向在线段OA上运动,以P为圆心,OP长为半径作⊙P;同时动点E以5个单位/秒的速度从点A出发,沿x轴的负半轴方向运动,过点E作EF⊥x轴,交射线AB于点F,以EF为边在EF的左侧作正方形EFMN,设运动时间为t秒.
如图,一次函数y=-$\frac{4}{5}$x+12与x轴、y轴相交于点A、B两点,动点P以4个单位/秒的速度从点O出发,沿OA方向在线段OA上运动,以P为圆心,OP长为半径作⊙P;同时动点E以5个单位/秒的速度从点A出发,沿x轴的负半轴方向运动,过点E作EF⊥x轴,交射线AB于点F,以EF为边在EF的左侧作正方形EFMN,设运动时间为t秒. 如图,AB为⊙O的直径,点C是$\widehat{AB}$上一点,点D为$\widehat{AC}$的中点,弦AC、BD交于点E,F为BD延长线上一点,且FA是⊙O的切线,
如图,AB为⊙O的直径,点C是$\widehat{AB}$上一点,点D为$\widehat{AC}$的中点,弦AC、BD交于点E,F为BD延长线上一点,且FA是⊙O的切线,