题目内容
17.某市在城中村改造中,需要种植A、B两种不同的树苗共3000棵,经招标,承包商以15万元的报价中标承包了这项工程,根据调查及相关资料表明,A、B两种树苗的成本价及成活率如表:| 品种 | 购买价(元/棵) | 成活率 |
| A | 28 | 90% |
| B | 40 | 95% |
(1)求y与x之间的函数关系式;
(2)政府要求栽植这批树苗的成活率不低于93%,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
分析 (1)根据题意和表格中的数据可以得到y与x的函数关系式;
(2)根据题意可以的得到相应的不等式,从而可以解答本题.
解答 解:(1)由题意可得,
y=150000-28x-40(3000-x)=30000+12x,
即y与x之间的函数关系式是y=12x+30000;
(2)由题意可得,
90%x+95%(3000-x)≥3000×93%,
解得,x≤1200,
∵y=12x+30000,
∴当x=1200时,y取得最大值,此时y=44400,
即承包商购买A种树苗1200棵,B种树苗1800棵时,能获得最大利润,最大利润是44400元.
点评 本题考查一次函数的应用、一元一次不等式的应用,解答本题的关键是明确题意,列出相应的方程和不等式.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
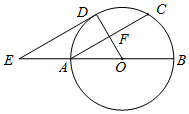 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.
如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E.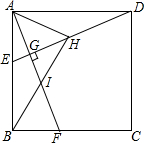 如图,正方形ABCD中,E,F分别为AB边,BC边上,且DE⊥AF于点G,H为线段DG上一点,连接AH,BH,BH交AF于点l,若∠GAH=45°,GI=1.正方形ABCD边长为4,则△AHD面积为$\sqrt{7}$-1.
如图,正方形ABCD中,E,F分别为AB边,BC边上,且DE⊥AF于点G,H为线段DG上一点,连接AH,BH,BH交AF于点l,若∠GAH=45°,GI=1.正方形ABCD边长为4,则△AHD面积为$\sqrt{7}$-1.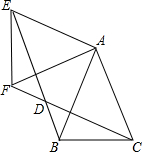 如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D
如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D