题目内容
3.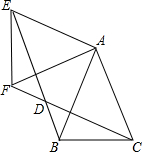 如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D
如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D(1)求证:BE=CF;
(2)当四边形ACDE为平行四边形时,求证:△ABE为等腰直角三角形.
分析 (1)先由旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,利用AB=AC可得AE=AF,于是根据旋转的定义,△AEB可由△AFC绕点A按顺时针方向旋转得到,然后根据旋转的性质得到BE=CD;
(2)首先证得△AFC为等腰直角三角形,然后即可证得△ABE为等腰直角三角形.
解答 解:(1)证明:∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC,
∴AE=AF,
∴△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴BE=CF;
(2)在□ABCD中,∠EAC+∠ACF=180°
∴∠EAF=∠BAC=45°
∴∠FAB+∠ACF=90°
又AF=AC
∴∠F=∠ACF
∴∠FAB+∠F=90°
∴∠ACF=45°
∴△AFC为等腰直角三角形
∴△ABE为等腰直角三角形
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了菱形的性质.

练习册系列答案
相关题目
17.某市在城中村改造中,需要种植A、B两种不同的树苗共3000棵,经招标,承包商以15万元的报价中标承包了这项工程,根据调查及相关资料表明,A、B两种树苗的成本价及成活率如表:
设种植A种树苗x棵,承包商获得的利润为y元.
(1)求y与x之间的函数关系式;
(2)政府要求栽植这批树苗的成活率不低于93%,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
| 品种 | 购买价(元/棵) | 成活率 |
| A | 28 | 90% |
| B | 40 | 95% |
(1)求y与x之间的函数关系式;
(2)政府要求栽植这批树苗的成活率不低于93%,承包商应如何选种树苗才能获得最大利润?最大利润是多少?
8.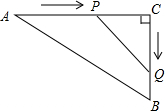 如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
 如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )
如图,在△ABC中,AC=50m,BC=40m,∠C=90°,点P从点A开始沿AC 边向点C以2m/s的速度匀速移动,同时另一点Q由C点开始以3m/s的速度沿着射线CB匀速移动,当△PCQ的面积等于300m2运动时间为( )| A. | 5秒 | B. | 20秒 | C. | 5秒或20秒 | D. | 不确定 |
15.若平面内有点A、B、C,过其中任意两点画直线,则最多可以画的条数是( )
| A. | 3条 | B. | 4条 | C. | 5条 | D. | 6条 |
12.如图所示的立体图形中,含有曲面的是( )


| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (2)(4) |
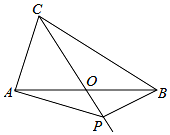 如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上在AB下方的一个动点,∠AOC=45°.则当△PAB为直角三角形时,AP的长为$\sqrt{18+9\sqrt{2}}$或=$\sqrt{18-9\sqrt{2}}$或3$\sqrt{5}$.
如图,在△ABC中,AB=BC=6,AO=BO,P是射线CO上在AB下方的一个动点,∠AOC=45°.则当△PAB为直角三角形时,AP的长为$\sqrt{18+9\sqrt{2}}$或=$\sqrt{18-9\sqrt{2}}$或3$\sqrt{5}$.