题目内容
某商场招募员工一名,现有甲、乙、丙三人竞聘.通过计算机技能、语言表达和商品知识三项测试,他们各自成绩(百分制)如下表:
(1)若商场需要招聘负责将商品拆装上架的人员,对计算机技能、语言表达和商品知识分别赋权2、3、5,计算这三名应试者的平均成绩.从成绩看,应该录取谁?
(2)若商场需要招聘电脑收银员,计算机技能、语言表达和商品知识成绩分别占50%、30%、20%,计算这三名应试者的平均成绩.从成绩看,应该录取谁?
| 应试者 | 计算机技能 | 语言表达 | 商品知识 |
| 甲 | 80 | 90 | 70 |
| 乙 | 70 | 80 | 90 |
| 丙 | 90 | 70 | 80 |
(2)若商场需要招聘电脑收银员,计算机技能、语言表达和商品知识成绩分别占50%、30%、20%,计算这三名应试者的平均成绩.从成绩看,应该录取谁?
考点:加权平均数
专题:
分析:(1)根据商品知识分别赋权2、3、5和各自的得分,分别进行计算,然后进行比较即可;
(2)根据加权平均数的计算公式分别列出算式,再进行计算即可.
(2)根据加权平均数的计算公式分别列出算式,再进行计算即可.
解答:解:(1)甲成绩:
=78(分),
乙成绩:
=73(分),
丙成绩:
=79(分),
因此丙成绩最高,应被录取.
(2)甲成绩:80×50%+90×30%+70×20%=81(分),
乙成绩:70×50%80×30%+90×20%=77(分),
丙成绩:90×50%+70×30%+80×20%=82(分),
因此丙成绩最高,应被录取.
| 80×2+90×3+70×5 |
| 2+3+5 |
乙成绩:
| 70×2+80×3+90×5 |
| 2+3+5 |
丙成绩:
| 90×2+70×3+80×5 |
| 2+3+5 |
因此丙成绩最高,应被录取.
(2)甲成绩:80×50%+90×30%+70×20%=81(分),
乙成绩:70×50%80×30%+90×20%=77(分),
丙成绩:90×50%+70×30%+80×20%=82(分),
因此丙成绩最高,应被录取.
点评:此题考查了加权平均数,掌握加权平均数的计算公式是本题的关键,是一道基础题.

练习册系列答案
相关题目
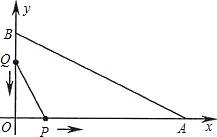 在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),
在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),
 如图,在矩形ABCD和正方形BEFG中,点G,B,C都在直线L上,点E在AB上,AB=5,AE=3,BC=10.
如图,在矩形ABCD和正方形BEFG中,点G,B,C都在直线L上,点E在AB上,AB=5,AE=3,BC=10.