题目内容
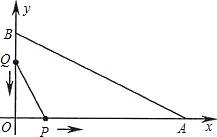 在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),
在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),(1)当t为何值时,四边形PABQ的面积为30cm2;
(2)当t为何值时,△POQ与△AOB相似.
考点:相似三角形的判定与性质
专题:动点型
分析:(1)根据P、Q的速度,用时间t表示出OQ和OP的长,即可通过三角形的面积公式得出三角形POQ的面积和t的关系式,然后用三角形AOB的面积减去三角形
POQ的面积即可;
(2)△POQ∽△AOB时,则
=
,根据对应边成比例即可求出t的值.
POQ的面积即可;
(2)△POQ∽△AOB时,则
| OQ |
| OB |
| OP |
| OA |
解答:解:(1)∵OA=12,OB=6,由题意,得BQ=1×t=t,OP=2×t=2t.
∴OQ=6-t.
∴30=
OA•OB-
×OP×OQ=
×12×6-
×2t(6-t),
解得t=3+
,或t=3-
∴当t为3+
,或t=3-
时四边形PABQ的面积为30cm2;
(2)若△POQ∽△AOB时,
=
,
即
=
,
整理得:6-t=t,
解得:t=3,
所以当t=3时,△POQ与△AOB相似.
∴OQ=6-t.
∴30=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得t=3+
| 3 |
| 3 |
∴当t为3+
| 3 |
| 3 |
(2)若△POQ∽△AOB时,
| OQ |
| OB |
| OP |
| OA |
即
| 6-t |
| 6 |
| 2t |
| 12 |
整理得:6-t=t,
解得:t=3,
所以当t=3时,△POQ与△AOB相似.
点评:本题主要考查了直角三角形的性质、相似三角形的判定和性质等知识点.

练习册系列答案
相关题目
 已知:如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,D为AC中点,E为AB上一点,AE=1,P为线段BD上一动点,则AP+EP的最小值为( )
已知:如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,D为AC中点,E为AB上一点,AE=1,P为线段BD上一动点,则AP+EP的最小值为( )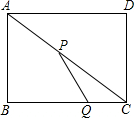 如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从A点出发,沿对角线AC向C移动,同时动点Q以1个单位/秒的速度从C点出发,沿CB向点B移动,当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.
如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从A点出发,沿对角线AC向C移动,同时动点Q以1个单位/秒的速度从C点出发,沿CB向点B移动,当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒. 在长形花坛ABCD中,P、Q两处是凉亭,要在花坛内建一个喷水池O,使O到AB、AD的距离相等,且到凉亭P、Q的距离也相等.
在长形花坛ABCD中,P、Q两处是凉亭,要在花坛内建一个喷水池O,使O到AB、AD的距离相等,且到凉亭P、Q的距离也相等.