题目内容
3.水是人类宝贵的资源.为鼓励居民节约用水,某市自来水公司对全市用户采用分段计费的方式计算水费,收费标准知下图所示.| 月用水量 | 不超过12t的部分 | 超过12t且不超过18t的部分 | 超过18t的部分 |
| 每吨收费标准(元) | 2 | 2.5 | 3 |
分析 设该用户5月的用水量为x吨,按x≤12、12<x≤18以及x>18三种情况分析,由前两种情况单价均不超过2.5元可知成立;当x>18时,根据总价=单价×用水量结合5月的水费平均不超过每吨2.5元,即可得出关于x的一元一次不等式,解之即可得出x的取值范围,取其最大值即可得出结论.
解答 解:设该用户5月的用水量为x吨,
当x≤12时,2<2.5,显然成立;
当12<x≤18时,2<2.5,2.5=2.5,一平均,显然成立;
当x>18时,有2×12+2.5×(18-12)+3(x-18)≤2.5x,
解得:18<x≤30.
答:该用户5月最多用水量为30吨.
点评 本题考查了一元一次不等式的应用,根据价=单价×用水量结合5月的水费平均不超过每吨2.5元,列出关于x的一元一次不等式是解题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
12. 如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )
如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )
 如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )
如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )| A. | y的最大值大于1 | B. | 当x=0时,y的值大于0 | ||
| C. | 当x=2时,y的值等于1 | D. | 当x>3时,y的值大于0 |
8.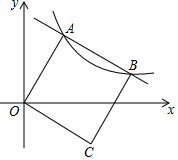 如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为( )
如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为( )
 如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为( )
如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
13.在下面的四个几何体中,左视图与主视图不完全相同的几何是( )
| A. |  正方体 | B. |  长方体 | C. |  球 | D. |  圆锥 |
 如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为9.
如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为9. 中国传统数学最重要的著作《九章算术》中记载:“今有牛五、羊二,直金十两:牛二、羊五,直金八两.问牛、羊各直金几何?”其译文是:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两,问每头牛、每只羊各值金多少两?”现设每头牛值金x两,每只羊值金y两,则可列方程组为$\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$.
中国传统数学最重要的著作《九章算术》中记载:“今有牛五、羊二,直金十两:牛二、羊五,直金八两.问牛、羊各直金几何?”其译文是:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两,问每头牛、每只羊各值金多少两?”现设每头牛值金x两,每只羊值金y两,则可列方程组为$\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$.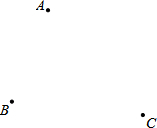 如图,平面上有三个点A,B,C,利用尺规按要求作图;
如图,平面上有三个点A,B,C,利用尺规按要求作图;