题目内容
20.已知等腰三角形ABC的腰AC上的中线BD把这个三角形的周长分成12cm,21cm的两部分,则这个三角形的腰AB的长为14cm.分析 因为题中没有指明两部分的具体值,故应该分两种情况进行分析,根据三角形的三边关系即可得到结论.
解答  解:∵点D是AC的中点,
解:∵点D是AC的中点,
∴AD=CD,
①当AB+AD=12cm时,AB=8cm,BC=17cm,因为8+8<17,所以不能构成三角形;
②当AB+AD=21cm时,AB=14cm,BC=5cm,因为14-5<14<14+5,所以能构成三角形;
∴腰长为14cm.
故答案为:14cm.
点评 此题主要考查等腰三角形的性质及三角形三边关系的综合运用.

练习册系列答案
相关题目
11.北京市某一周的最高气温统计如表:
则这组数据的平均数是30,中位数是30.
| 日期 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 最高气温(℃) | 31 | 29 | 28 | 30 | 31 | 30 | 31 |
12. 如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )
如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )
 如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )
如图,二次函数y=ax2+bx+c的图象经过点(1,1)和点(3,0).下列关于这个二次函数的描述,正确的是( )| A. | y的最大值大于1 | B. | 当x=0时,y的值大于0 | ||
| C. | 当x=2时,y的值等于1 | D. | 当x>3时,y的值大于0 |
8.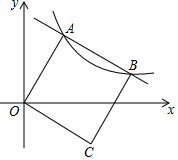 如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为( )
如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为( )
 如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为( )
如图,平面直角坐标系中,O为坐标原点,正方形OABC的定点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
9.一幅平面图的比例尺是10:1,实际距离1厘米在这幅图上应画( )
| A. | 1毫米 | B. | 1厘米 | C. | 1分米 | D. | 10分米 |
10.在0,2,3,(-5)0这四个数中,最大的数是( )
| A. | 0 | B. | 2 | C. | 3 | D. | (-5)0 |
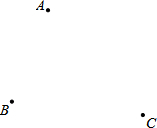 如图,平面上有三个点A,B,C,利用尺规按要求作图;
如图,平面上有三个点A,B,C,利用尺规按要求作图;