题目内容
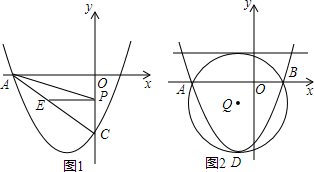
17.如图,已知抛物线y=mx2+2mx+c(m≠0),与y轴交于点C(0,-4),与x轴交于点A(-4,0)和点B.(1)求该抛物线的解析式;
(2)若P是线段OC上的动点,过点P作PE∥OA,交AC于点E,连接AP,当△AEP的面积最大时,求此时点P的坐标;
(3)点D为该抛物线的顶点,⊙Q为△ABD的外接圆,求证⊙Q与直线y=2相切.
分析 审题知:(1)题中已知抛物线上的两个点,只需将点坐标代入抛物线解析式即可求解;
(2)此题只需设出点P的坐标(0,t),并根据题中关系,列出△AEP面积关于t的二次函数即可求解;
(3)此题应先求出圆心Q的坐标,在求出半径,证明圆心到直线的距离等于半径即可.
解答 解:(1)把点C(0,-4),点A(-4,0)坐标代入:y=mx2+2mx+c(m≠0)得:$\left\{\begin{array}{l}{-4=c}\\{0=16m-8m+c}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{c=-4}\\{m=\frac{1}{2}}\end{array}\right.$.
所以:抛物线的解析式为:y=$\frac{1}{2}$x2+x-4.
(2)设点P(0,t)-4≤t≤0,则有:PC=t+4,OP=-t,OA=4
由PE∥OA可知:三角形CPE,三角形POA,三角形AOC均为直角三角形,
所以:$\frac{PE}{OA}=\frac{PC}{OC}$,$\frac{PE}{4}=\frac{t+4}{4}$,解得:PE=t+4
所以:S△AEP=$\frac{1}{2}$×OA×OC-$\frac{1}{2}$×OA×OP-$\frac{1}{2}$×PC×PE
=$\frac{1}{2}$×4×4-$\frac{1}{2}$×4×(-t)-$\frac{1}{2}$×(t+4)×(t+4)
=-$\frac{1}{2}$t2-2t.
所以:当t=-$\frac{-2}{2×(-\frac{1}{2})}$=-2时,△AEP的面积最大,
此时:P(0,-2);
(3)过点D作DM⊥x轴,垂足为M,
抛物线的解析式为:y=$\frac{1}{2}$x2+x-4=$\frac{1}{2}$(x+1)2-$\frac{9}{2}$
所以:顶点D(-1,$\frac{9}{2}$),点M(-1,0),AM=-1-(-4)=3
由圆和抛物线的对称性可知:圆心Q在DM上,QM⊥AB,
设圆Q的半径为r,则AQ=r,QM=$\frac{9}{2}$-r,由勾股定理得:
r2=${(\frac{9}{2}-r)}^{2}$+32,解得:r=$\frac{13}{4}$,QM=$\frac{9}{2}$-r=$\frac{5}{4}$,所以点Q(-1,-$\frac{5}{4}$)
因为直线y=2与x轴平行,所以点Q到直线y=2的距离为:2-(-$\frac{5}{4}$)=$\frac{13}{4}$,
所以:圆心Q到直线y=2的距离=圆的半径
所以:⊙Q与直线y=2相切.
点评 此题主要考察抛物线的形积问题,把点坐标代入求解析式要认真,在关于最大面积问题,一般要建立二次函数,在证明相切时,抓住圆心到直线的距离等于半径是证明的关键.

| A. | 点(-7,3) | B. | 点(3,7) | C. | 点(4,-8) | D. | 点(2.5,1.5) |
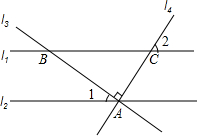 如图,已知直线l1∥l2,直线l3⊥l4于A,在l2上,若∠1=27°,则∠2的度数为( )
如图,已知直线l1∥l2,直线l3⊥l4于A,在l2上,若∠1=27°,则∠2的度数为( )| A. | 27° | B. | 53° | C. | 63° | D. | 54° |
| A. | 正方形是轴对称图形且有四条对称轴 | |
| B. | 平行四边形的对角线垂直平分 | |
| C. | 矩形的对角线互相垂直 | |
| D. | 菱形的对角线相等 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |

| A. | 3a1+4a2+3a3 | B. | 3a1+3a2+3a3 | C. | 4a1+3a2+4a3 | D. | 4a1+4a2+4a3 |