题目内容
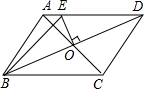 如图所示,在四边形ABCD中,AB=DC,AD=BC,对角线AC,BD相交于点O,EO垂直平分BD,△ABE的周长为12cm,则四边形ABCD的周长为
如图所示,在四边形ABCD中,AB=DC,AD=BC,对角线AC,BD相交于点O,EO垂直平分BD,△ABE的周长为12cm,则四边形ABCD的周长为考点:平行四边形的性质,线段垂直平分线的性质
专题:
分析:根据平行四边形的性质,两组对边分别平行且相等,对角线相互平分,OE⊥BD可说明EO是线段BD的中垂线,中垂线上任意一点到线段两端点的距离相等,则BE=DE,再利用线段间的等量关系可证明平行四边形ABCD的周长是△ABE的周长的2倍.
解答:解:∵?ABCD中,
∴点O平分BD、AC,即OB=OD,
又∵OE⊥BD,
∴OE是线段BD的中垂线,
∴BE=DE,
∴AE+ED=AE+BE,
∴AB+AD=AB+AE+BE=△ABE的周长=12cm,
∴?ABCD的周长=2(AB+AD)=2×12=24cm.
故答案为:24cm.
∴点O平分BD、AC,即OB=OD,
又∵OE⊥BD,
∴OE是线段BD的中垂线,
∴BE=DE,
∴AE+ED=AE+BE,
∴AB+AD=AB+AE+BE=△ABE的周长=12cm,
∴?ABCD的周长=2(AB+AD)=2×12=24cm.
故答案为:24cm.
点评:此题主要考查了平行四边形的性质及全等三角形的判定及性质,还利用了中垂线的判定及性质等,考查面积较广,有一定的综合性.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
下列各数与2的和是0的是( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 如图,直线l1∥l2,AB⊥CD,∠1=30°,∠2的度数=
如图,直线l1∥l2,AB⊥CD,∠1=30°,∠2的度数= 如图,在平面直角坐标系中,点0为坐标原点,△ABC的顶点B、C的坐标分别为(-2,O)、(3,O),顶点A在y轴的正半轴上,△ABC的高BD交线段DA于点E,且AD=BD.
如图,在平面直角坐标系中,点0为坐标原点,△ABC的顶点B、C的坐标分别为(-2,O)、(3,O),顶点A在y轴的正半轴上,△ABC的高BD交线段DA于点E,且AD=BD.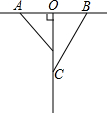 如图所示,AO=BO=50cm,OC是一条射线,OC⊥AB于点O,一只甲虫由点A以2cm/s的速度向B爬行,同时另一只甲虫由点O以3cm/s的速度沿OC方向爬行,是否存在这样的时刻,使两只甲虫与点O组成的三角形的面积为450cm2?若存在,请说明在什么时刻;若不存在,请说明理由.
如图所示,AO=BO=50cm,OC是一条射线,OC⊥AB于点O,一只甲虫由点A以2cm/s的速度向B爬行,同时另一只甲虫由点O以3cm/s的速度沿OC方向爬行,是否存在这样的时刻,使两只甲虫与点O组成的三角形的面积为450cm2?若存在,请说明在什么时刻;若不存在,请说明理由. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF,其中正确的序号是
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF,其中正确的序号是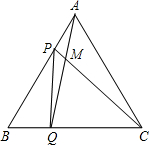 如图,点P、Q分别是边长是4cm的等边△ABC的边AB、BC上的动点,点P从顶点A出发沿着路线A→B→C→A做匀速运动,同时,点Q从顶点B出发,沿着路线B→C→A→B做匀速运动,且点P,Q的速度都为1cm/s,设运动时间为t秒
如图,点P、Q分别是边长是4cm的等边△ABC的边AB、BC上的动点,点P从顶点A出发沿着路线A→B→C→A做匀速运动,同时,点Q从顶点B出发,沿着路线B→C→A→B做匀速运动,且点P,Q的速度都为1cm/s,设运动时间为t秒