题目内容
(1)计算:(3
-2
+
)÷2
.
(2)解方程:x(3x-2)=2(3x-2).
| 12 |
|
| 48 |
| 3 |
(2)解方程:x(3x-2)=2(3x-2).
考点:二次根式的混合运算,解一元二次方程-因式分解法
专题:
分析:(1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先移项得到x(3x-2)-2(3x-2)=0,然后利用因式分解法解方程.
(2)先移项得到x(3x-2)-2(3x-2)=0,然后利用因式分解法解方程.
解答:解:(1)原式=(6
-
+4
)÷2
=
÷2
=
;
(2)x(3x-2)-2(3x-2)=0,
(3x-2)(x-2)=0,
3x-2=0或x-2=0,
所以x1=
,x2=2.
| 3 |
2
| ||
| 3 |
| 3 |
| 3 |
=
28
| ||
| 3 |
| 3 |
=
| 14 |
| 3 |
(2)x(3x-2)-2(3x-2)=0,
(3x-2)(x-2)=0,
3x-2=0或x-2=0,
所以x1=
| 2 |
| 3 |
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,然后进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了因式分解法解一元二次方程.

练习册系列答案
相关题目
下列说法不正确的是( )
| A、绝对值等于本身的数是正数 |
| B、倒数等于本身的数有2个 |
| C、有理数可分为整数和分数 |
| D、0既不是正数,也不是负数 |
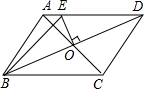 如图所示,在四边形ABCD中,AB=DC,AD=BC,对角线AC,BD相交于点O,EO垂直平分BD,△ABE的周长为12cm,则四边形ABCD的周长为
如图所示,在四边形ABCD中,AB=DC,AD=BC,对角线AC,BD相交于点O,EO垂直平分BD,△ABE的周长为12cm,则四边形ABCD的周长为