��Ŀ����
 ��ͼ����ƽ��ֱ������ϵ�У���0Ϊ����ԭ�㣬��ABC�Ķ���B��C������ֱ�Ϊ��-2��O������3��O��������A��y����������ϣ���ABC�ĸ�BD���߶�DA�ڵ�E����AD=BD��
��ͼ����ƽ��ֱ������ϵ�У���0Ϊ����ԭ�㣬��ABC�Ķ���B��C������ֱ�Ϊ��-2��O������3��O��������A��y����������ϣ���ABC�ĸ�BD���߶�DA�ڵ�E����AD=BD����1�����߶�AE�ij���
��2������P�ӵ�E�������߶�EA��ÿ��1����λ���ȵ��ٶ����յ�A�˶�������Q�ӵ�B����������BC��ÿ��4����λ���ȵ��ٶ��˶���P��Q����ͬʱ�������ҵ�P����A�㴦ʱP��Q����ͬʱֹͣ�˶������P���˶�ʱ��Ϊt�룬��PEQ�����ΪS�����ú�t��ʽ�ӱ�ʾS��ֱ��д����Ӧ��t��ȡֵ��Χ��
��3���ڣ�2���ʵ������£���F��ֱ��AC�ϵ�һ����CF=BE���Ƿ����tֵ��ʹ�Ե�B��E��PΪ��������������Ե�F��C��QΪ�����������ȫ�ȣ������ڣ����������������tֵ���������ڣ���˵�����ɣ�
���㣺ȫ�������ε��ж�������,������ͼ������
ר�⣺������
��������1����֤��OAC=��CBD������֤����AED�ա�BCD���ɵ�AE=BC�����ɽ��⣻
��2���������ۣ��ٵ���Q���߶�BO��ʱ������S=
PE•OQ���ɽ��⣻
�ڵ���Q���߶�BO���ӳ�����ʱ������S=
PE•OQ���ɽ��⣻
��3��������������ٵ���F���߶�AC���ӳ�����ʱ����t�ֱ��ʾPE��QC������PE=QC�������t��ֵ�����ɽ��⣬
�ڵ���F���߶�AC��ʱ����ͼ4������F��D�غϣ���t�ֱ��ʾPE��QC������PE=QC�������t��ֵ�����ɽ��⣮
��2���������ۣ��ٵ���Q���߶�BO��ʱ������S=
| 1 |
| 2 |
�ڵ���Q���߶�BO���ӳ�����ʱ������S=
| 1 |
| 2 |
��3��������������ٵ���F���߶�AC���ӳ�����ʱ����t�ֱ��ʾPE��QC������PE=QC�������t��ֵ�����ɽ��⣬
�ڵ���F���߶�AC��ʱ����ͼ4������F��D�غϣ���t�ֱ��ʾPE��QC������PE=QC�������t��ֵ�����ɽ��⣮
����⣺��1����BD��AC��
���ADE=��BDC=90�㣬
���CBD+��ACB=90�㣬
�ߡ�AOC=90�㣬
���OAC+��ACB=90�㣬
���OAC=��CBD��
�ڡ�AED�͡�BCD�У�
��
���AED�ա�BCD��ASA����
��AE=BC��
��B��-2��0����C��3��0��
��BC=5��
��AE=5��
��2���������ۣ��ٵ���Q���߶�BO��ʱ������ͼ1��
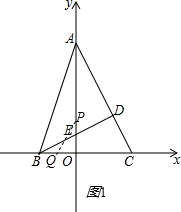
S=
PE•OQ=
t��2-4t��=-2t2+t����0��t��
����
�ڵ���Q���߶�BO���ӳ�����ʱ������ͼ2��
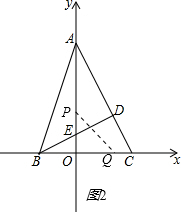
S=
PE•OQ=
t��4t-2��=2t2-t����
��t��5����
��3�������������
�ٵ���F���߶�AC���ӳ�����ʱ����ͼ3��
��֪��BEP=��FCQ��BE=CF����ʱ���ڡ�PBE�ա�QCF��
��PE=QC��
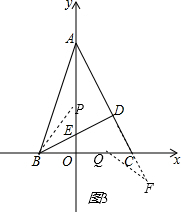
��ʱCQ=5-4t��PE=t��
��5-4t=t��
��ã�t=1��
�ڵ���F���߶�AC��ʱ����ͼ4������F��D�غϣ�
��֪��BEP=��FCQ��BE=CF����ʱ���ڡ�PBE�ա�QCF��
��PE=QC��
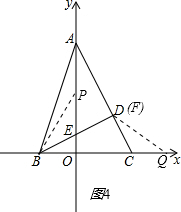
��ʱCQ=4t-5��PE=t��
��4t-5=t��
��ã�t=
��
���ADE=��BDC=90�㣬
���CBD+��ACB=90�㣬
�ߡ�AOC=90�㣬
���OAC+��ACB=90�㣬
���OAC=��CBD��
�ڡ�AED�͡�BCD�У�
|
���AED�ա�BCD��ASA����
��AE=BC��
��B��-2��0����C��3��0��
��BC=5��
��AE=5��
��2���������ۣ��ٵ���Q���߶�BO��ʱ������ͼ1��

S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
�ڵ���Q���߶�BO���ӳ�����ʱ������ͼ2��

S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��3�������������
�ٵ���F���߶�AC���ӳ�����ʱ����ͼ3��
��֪��BEP=��FCQ��BE=CF����ʱ���ڡ�PBE�ա�QCF��
��PE=QC��

��ʱCQ=5-4t��PE=t��
��5-4t=t��
��ã�t=1��
�ڵ���F���߶�AC��ʱ����ͼ4������F��D�غϣ�
��֪��BEP=��FCQ��BE=CF����ʱ���ڡ�PBE�ա�QCF��
��PE=QC��

��ʱCQ=4t-5��PE=t��
��4t-5=t��
��ã�t=
| 5 |
| 3 |
���������⿼����ȫ�������ε��ж���������ȫ�������ζ�Ӧ����ȵ����ʣ���������֤��AED�ա�BCD�ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
��֪a=10��b=9�������ʽ4a-4b-3��ֵΪ��������
| A��1 | B��-1 | C��7 | D��-7 |
���ij���õ��������ҵ��¶���5�棬�䶳�ҵ��¶ȱ�����ҵ��¶ȵ�20�棬���䶳�ҵ��¶�Ϊ��������
| A��-25�� | B��-20�� |
| C��-15�� | D��-10�� |
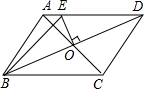 ��ͼ��ʾ�����ı���ABCD�У�AB=DC��AD=BC���Խ���AC��BD�ཻ�ڵ�O��EO��ֱƽ��BD����ABE���ܳ�Ϊ12cm�����ı���ABCD���ܳ�Ϊ
��ͼ��ʾ�����ı���ABCD�У�AB=DC��AD=BC���Խ���AC��BD�ཻ�ڵ�O��EO��ֱƽ��BD����ABE���ܳ�Ϊ12cm�����ı���ABCD���ܳ�Ϊ