题目内容
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF,其中正确的序号是
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上,下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF,其中正确的序号是考点:全等三角形的判定与性质,等边三角形的性质,正方形的性质
专题:
分析:易证△ABE≌△ADF,可得∠BAE=∠DAF,BE=DF,即可求得①②正确,再根据DF≠
AF即可求得③错误,即可解题.
| 1 |
| 2 |
解答:解:在△ABE和△ADF中,
,
∴△ABE≌△ADF(HL),
∴∠BAE=∠DAF,BE=DF,
∵CD=BC,∴CE=CF,①正确;
∵∠BAD=90°,∠EAF=60°,
∴∠BAE=∠DAF=15°,
∴∠AEB=90°-15°=75°,②正确;
∵sin15°≠
,
∴DF≠
AF,
∴BE+DF=2DF≠AF,
∵AF=EF,
∴BE+DF≠EF.③错误;
故答案为:①②.
|
∴△ABE≌△ADF(HL),
∴∠BAE=∠DAF,BE=DF,
∵CD=BC,∴CE=CF,①正确;
∵∠BAD=90°,∠EAF=60°,
∴∠BAE=∠DAF=15°,
∴∠AEB=90°-15°=75°,②正确;
∵sin15°≠
| 1 |
| 2 |
∴DF≠
| 1 |
| 2 |
∴BE+DF=2DF≠AF,
∵AF=EF,
∴BE+DF≠EF.③错误;
故答案为:①②.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ABE≌△ADF是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法不正确的是( )
| A、绝对值等于本身的数是正数 |
| B、倒数等于本身的数有2个 |
| C、有理数可分为整数和分数 |
| D、0既不是正数,也不是负数 |
下列命题中是假命题的是( )
| A、平行四边形的对边相等 |
| B、菱形的四条边相等 |
| C、矩形的对边平行且相等 |
| D、平行四边形的对角线相等 |
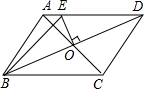 如图所示,在四边形ABCD中,AB=DC,AD=BC,对角线AC,BD相交于点O,EO垂直平分BD,△ABE的周长为12cm,则四边形ABCD的周长为
如图所示,在四边形ABCD中,AB=DC,AD=BC,对角线AC,BD相交于点O,EO垂直平分BD,△ABE的周长为12cm,则四边形ABCD的周长为 已知,如图,在△ABC中,内切圆I与边BC,CA,AB分别相交于点D,E,F.求证:∠FDE=90°-
已知,如图,在△ABC中,内切圆I与边BC,CA,AB分别相交于点D,E,F.求证:∠FDE=90°-