题目内容
 已知:如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,D为AC中点,E为AB上一点,AE=1,P为线段BD上一动点,则AP+EP的最小值为( )
已知:如图,在Rt△ABC中,∠ABC=90°,AB=BC=4,D为AC中点,E为AB上一点,AE=1,P为线段BD上一动点,则AP+EP的最小值为( )A、3
| ||
| B、5 | ||
C、4
| ||
| D、6 |
考点:轴对称-最短路线问题
专题:
分析:连接CE交BD于F,由等腰直角三角形的性质和已知条件可知A和C关于D对称,所以P在F时,AP+PE最小为CE的长,再根据勾股定理即可求出CE的长即可.
解答:解:连接CE交BD于F,
∵∠ABC=90°,AB=BC=4,D为AC中点,
∴BD⊥AC,
∴A和C关于D对称,
∴AF=CF,
∴EF+CF=AF+CF=CE,
∵AE=1,
∴BE=3,
∴CE=
=5,
故选B.
∵∠ABC=90°,AB=BC=4,D为AC中点,

∴BD⊥AC,
∴A和C关于D对称,
∴AF=CF,
∴EF+CF=AF+CF=CE,
∵AE=1,
∴BE=3,
∴CE=
| 32+42 |
故选B.
点评:本题考查了轴对称-最短路线问题,用到的知识点由等腰直角三角形的性质、勾股定理,凡是涉及最短距离的问题,一般要考虑线段的性质定理,利用轴对称变换来解决,多数情况要作点关于某直线的对称点.

练习册系列答案
相关题目
如图,某种自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm,如果这种型号自行车的链条(没有安装前)共有60节组成,那么链条的总长度是( )


| A、100cm |
| B、85.8cm |
| C、85cm |
| D、102.8cm |
下列调查适合用全面调查方式的是( )
| A、了解黑龙江省居民年人均收入 |
| B、了解北京市中小学生的近视率 |
| C、调查2014年足球世界杯的收视率 |
| D、了解某班学生的身高情况 |
下列计算错误的是( )
| A、(a2b3)2=a4b6 |
| B、(a5)2=a10 |
| C、4x2y•(-3x4y3)=-12x6y3 |
| D、2x•(3x2-x+5)=6x3-2x2+10x |
若0≤a≤1,则
+
=( )
| a2 |
| (a-1)2 |
| A、2a-1 | B、1 |
| C、-1 | D、-2a+1 |
下列命题中,是真命题的是( )
| A、同位角相等 |
| B、有且只有一条直线与已知直线垂直 |
| C、相等的角是对顶角 |
| D、邻补角一定互补 |
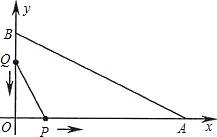 在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),
在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),