题目内容
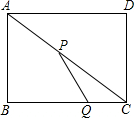 如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从A点出发,沿对角线AC向C移动,同时动点Q以1个单位/秒的速度从C点出发,沿CB向点B移动,当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.
如图,在矩形ABCD中,AB=6,BC=8,动点P以2个单位/秒的速度从A点出发,沿对角线AC向C移动,同时动点Q以1个单位/秒的速度从C点出发,沿CB向点B移动,当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)求△CPQ的面积S与时间t之间的函数关系式;
(2)以P为圆心,PA为半径的圆与以Q为圆心,QC为半径的圆相切时,求出t的值;
(3)在P、Q移动的过程中,当△CPQ为等腰三角形时,直接写出t的值.
考点:相似形综合题
专题:
分析:(1)根据相似三角形的判定与性质,可得PF的长,根据三角形的面积公式,可得答案;
(2)分类讨论,外切,内切,
根据相似三角形的性质,可得PF、FC的长,根据勾股定理,可得PQ的长,根据相切时PQ的两种表达方式,可得方程,根据解方程,可得答案;
(3)根据等腰三角形的定义,分类讨论:PC=QC,PQ=QC,PQ=PC,可得方程,根据解方程,可得答案.
(2)分类讨论,外切,内切,
根据相似三角形的性质,可得PF、FC的长,根据勾股定理,可得PQ的长,根据相切时PQ的两种表达方式,可得方程,根据解方程,可得答案;
(3)根据等腰三角形的定义,分类讨论:PC=QC,PQ=QC,PQ=PC,可得方程,根据解方程,可得答案.
解答:解:在矩形ABCD中,∠B=90°,AB=6,BC=8,
则AC=10,
由题意得:AP=2t,CP=10-2t,CQ=t,
(1)
过点P作PF⊥BC于F,
可得△CPF∽△CAB,
∴
=
,即
=
,
∴PF=6-
t,
∴S=
×QC×PF=-
t2+3t(0≤t≤5).
(2)∵△PCF∽△ACB,
∴
=
=
,
即
=
=
,
∴PF=6-
t,
FC=8-
t,
则在Rt△PFQ中,
PQ2=PF2+FQ2=(6-
t)2+(8-
t-t)2=
t2-56t+100.
①当⊙P与⊙Q外切时,有PQ=PA+QC=3t,
此时PQ2=
t2-56t+100=9t2,
整理得:t2+70t-125=0,
解得t1=15
-35,t2=-15
-35(舍去).
②当⊙P与⊙Q内切时,有PQ=PA-QC=t,
此时PQ2=
t2-56t+100=t2,整理得:
9t2-70t+125=0,
解得t1=
,t2=5.
综上所述:⊙P与⊙Q相切时t=
或t=5或t=15
-35;
(3)10-2t=t,
t=
秒(此时PC=QC),
t2-56t+100=t2
t=
秒(此时PQ=QC),
t2-56t+100=(10-2t)2
t=
秒(此时PQ=PC)△CPQ为等腰三角形.
则AC=10,
由题意得:AP=2t,CP=10-2t,CQ=t,
(1)

过点P作PF⊥BC于F,
可得△CPF∽△CAB,
∴
| PF |
| AB |
| CP |
| CA |
| PF |
| 6 |
| 10-2t |
| 10 |
∴PF=6-
| 6 |
| 5 |
∴S=
| 1 |
| 2 |
| 3 |
| 5 |
(2)∵△PCF∽△ACB,
∴
| PF |
| AB |
| PC |
| AC |
| FC |
| BC |
即
| PF |
| 6 |
| 10-2t |
| 10 |
| FC |
| 8 |
∴PF=6-
| 6 |
| 5 |
FC=8-
| 8 |
| 5 |
则在Rt△PFQ中,
PQ2=PF2+FQ2=(6-
| 6 |
| 5 |
| 8 |
| 5 |
| 41 |
| 5 |
①当⊙P与⊙Q外切时,有PQ=PA+QC=3t,
此时PQ2=
| 41 |
| 5 |
整理得:t2+70t-125=0,
解得t1=15
| 6 |
| 6 |
②当⊙P与⊙Q内切时,有PQ=PA-QC=t,
此时PQ2=
| 41 |
| 5 |
9t2-70t+125=0,
解得t1=
| 25 |
| 9 |
综上所述:⊙P与⊙Q相切时t=
| 25 |
| 9 |
| 6 |
(3)10-2t=t,
t=
| 10 |
| 3 |
| 41 |
| 5 |
t=
| 25 |
| 9 |
| 41 |
| 5 |
t=
| 80 |
| 21 |
点评:本题考查了相似形综合题,利用了相似三角形的判定与性质,两圆相切的关系,解一元二次方程,分类讨论是解题关键,题目有难度,注意要把不符合题意的解舍去.

练习册系列答案
相关题目
下列计算错误的是( )
| A、(a2b3)2=a4b6 |
| B、(a5)2=a10 |
| C、4x2y•(-3x4y3)=-12x6y3 |
| D、2x•(3x2-x+5)=6x3-2x2+10x |

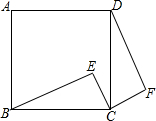 如图,点E是正方形ABCD内的一点,将△BEC绕点C顺时针旋转至△DFC.
如图,点E是正方形ABCD内的一点,将△BEC绕点C顺时针旋转至△DFC.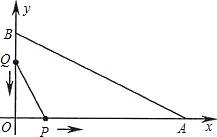 在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),
在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),
 直线m表示一条公路,公路两旁分别有两个村庄A和B,要在公路上建一个临时车站P,使它到两个村庄距离之和最小,车站P应建在什么位置?在图中画出车站的位置,并说明这样的理由.
直线m表示一条公路,公路两旁分别有两个村庄A和B,要在公路上建一个临时车站P,使它到两个村庄距离之和最小,车站P应建在什么位置?在图中画出车站的位置,并说明这样的理由.