题目内容
15. 如下数表是由从1开始的连续自然数组成的,则第10行各数之和1729.
如下数表是由从1开始的连续自然数组成的,则第10行各数之和1729.
分析 由数列知第n行最后一数为n2,则第一个数为n2-2n+2,每行数的个数为1,3,5,…的奇数列,从而得第n行各数之和为$\frac{{n}^{2}-2n+2+{n}^{2}}{2}$×(2n-1)=(n2-n+1)(2n-1),将n=10代入以上列式从而解得.
解答 解:第n行最后一数为n2,则第一个数为n2-2n+2,
每行数由题意知每行数的个数为1,3,5,…的奇数列,
第n行共有2n-1个;
第n行各数之和:$\frac{{n}^{2}-2n+2+{n}^{2}}{2}$×(2n-1)=(n2-n+1)(2n-1).
当n=10时,(n2-n+1)(2n-1)=(102-10+1)(2×10-1)=1729,
故答案为:1729.
点评 此题考查数字变化的规律,通过观察,分析、归纳并发现规律:每行最后一个数为行数的平方,每行数的个数是行数的2倍与1的差是本题的关键.

练习册系列答案
相关题目
10.一个双肩背书包的标价为a元,现按标价八折出售,则售价是( )
| A. | 8a元 | B. | 2a元 | C. | 0.8a元 | D. | 0.2a元 |
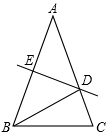 如图,在△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB、AC于E、D两点.
如图,在△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB、AC于E、D两点.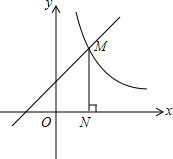 如图,一次函数y=x+1的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1.
如图,一次函数y=x+1的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1. 将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=40°,∠2=50°,那么∠3的度数等于12°.
将等边三角形、正方形、正五边形按如图所示的位置摆放,如果∠1=40°,∠2=50°,那么∠3的度数等于12°.