题目内容
14. 如图,已知反比例函数y=$\frac{2}{x}$的图象上有一组点B1,B2,…Bn,它们的横坐标依次增加1,且点B1横坐标为1.“①,②,③…”分别表示如图所示的三角形的面积,记S1=①-②,S2=②-③,…,S1+S2+…+Sn=$\frac{n}{n+1}$(用含n的式子表示).
如图,已知反比例函数y=$\frac{2}{x}$的图象上有一组点B1,B2,…Bn,它们的横坐标依次增加1,且点B1横坐标为1.“①,②,③…”分别表示如图所示的三角形的面积,记S1=①-②,S2=②-③,…,S1+S2+…+Sn=$\frac{n}{n+1}$(用含n的式子表示).
分析 先根据规律得出①,②,③…的值,并依次求S1、S2、Sn的值,再相加即可.
解答 解:由题意得:①=$\frac{1}{2}$×2=1,
②=$\frac{1}{2}$×1=$\frac{1}{2}$,
③=$\frac{1}{3}$,
④=$\frac{1}{4}$,
… ,
, ,
,
∴S1=①-②=1-$\frac{1}{2}$,
S2=②-③=$\frac{1}{2}-\frac{1}{3}$,
S3=③-④=$\frac{1}{3}-\frac{1}{4}$,
… ;
;
∴S1+S2+…+Sn=①-②+②-③+③-④+…=1-$\frac{1}{2}$+$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}-\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
故答案为:$\frac{n}{n+1}$.
点评 本题考查了反比例函数系数k的几何意义、反比例函数的性质,解题的关键是明确题意,找出所求三角形面积的特点,利用数形结合的思想解答问题.明确在反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
4.测得某弹簧的长度y(cm)与挂重x(kg)之间的关系如下表(该弹簧挂重不超过20kg):
(1)写出y与x的关系;
(2)由(1)计算当弹簧长度为5.6cm时的弹簧挂重.
| x/kg | 0 | 1 | 2 | 3 | … |
| y/cm | 4 | 4.2 | 4.4 | 4.6 | … |
(2)由(1)计算当弹簧长度为5.6cm时的弹簧挂重.
9.下列运算错误的是( )
| A. | 2b+5b=7b | B. | (b2)5=b10 | C. | b2•b3=b7 | D. | b9÷b3=b3 |
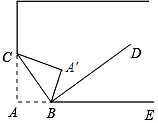 如图,将书角斜折过去,使角顶点落在A′处,BC为折痕,∠A′BD=∠DBE,求∠CBD的度数.
如图,将书角斜折过去,使角顶点落在A′处,BC为折痕,∠A′BD=∠DBE,求∠CBD的度数.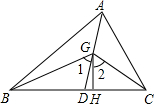 如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证:
如图,在△ABC中,AD是它的角平分线,G是AD上的一点,BG,CG分别平分∠ABC,∠ACB,GH⊥BC,垂足为H,求证: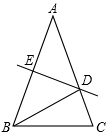 如图,在△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB、AC于E、D两点.
如图,在△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB、AC于E、D两点.