题目内容
18.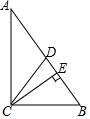 如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,CE⊥AB于E,AC=8,BC=6,则DE=1.4.
如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,CE⊥AB于E,AC=8,BC=6,则DE=1.4.
分析 在Rt△ABC中,利用勾股定理可求AB=10,由于直角三角形斜边上的中线等于斜边的一半,易求CD=5,再根据三角形面积公式可求CE,再由勾股定理求出DE即可.
解答 解:在Rt△ABC中,AB2=AC2+BC2=100,
∴AB=10,
∵CD是△ABC的中线,
∴CD=$\frac{1}{2}$AB=5,
∵S△ABC=$\frac{1}{2}$×6×8=$\frac{1}{2}$×10•CE,
∴CE=4.8,
∴在Rt△CDE中,DE=$\sqrt{C{D}^{2}-C{E}^{2}}$=$\sqrt{{5}^{2}-4.{8}^{2}}$=1.4;
故答案为:1.4.
点评 本题考查了勾股定理、直角三角形斜边上的中线性质、三角形面积的计算;熟练掌握勾股定理是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列运算错误的是( )
| A. | 2b+5b=7b | B. | (b2)5=b10 | C. | b2•b3=b7 | D. | b9÷b3=b3 |
13.一次函数y=-2x+6与x轴的交点坐标是( )
| A. | (3,0) | B. | (-3,0) | C. | (0,3) | D. | (0,-3) |
10.一个双肩背书包的标价为a元,现按标价八折出售,则售价是( )
| A. | 8a元 | B. | 2a元 | C. | 0.8a元 | D. | 0.2a元 |
8.已知一次函数y=(m-1)x-4的图象经过(2,4),则m的值为( )
| A. | 7 | B. | 5 | C. | 8 | D. | 2 |
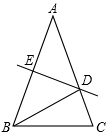 如图,在△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB、AC于E、D两点.
如图,在△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB、AC于E、D两点.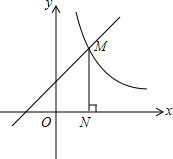 如图,一次函数y=x+1的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1.
如图,一次函数y=x+1的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1.