题目内容
设菱形的周长为20,两条对角线的长是方程x2-(2m-1)x+4m-4=0的两个根,则m的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
| D、以上答案都不对 |
考点:根与系数的关系,解一元二次方程-因式分解法,勾股定理,菱形的性质
专题:综合题,数形结合
分析:先根据菱形的四边相等及周长公式求出此菱形的边长为5.设菱形ABCD的两条对角线长分别为α,β,那么由根与系数的关系,可得α+β=2m-1①,α•β=4m-4②.再根据菱形的对角线互相垂直平分及勾股定理可知,(
)2+(
)2=52,把①②两式分别代入,得到一个关于m的一元二次方程,运用因式分解法求出此方程的根,最后根据判别式及α,β表示的实际意义确定m的值.
| α |
| 2 |
| β |
| 2 |
解答: 解:如图.∵菱形ABCD的周长为20,
解:如图.∵菱形ABCD的周长为20,
∴AB=5.
设菱形ABCD的两条对角线长分别为α,β,则α,β是方程x2-(2m-1)x+4m-4=0的两个根,
∴α+β=2m-1 ①,α•β=4m-4 ②.
∵在菱形ABCD中,AC⊥BD,AO=OC,BO=OD,
∴OA2+OB2=AB2,
即(
)2+(
)2=52,
∴α2+β2=100,
∴(α+β)2-2αβ=100,
把①②两式分别代入,得(2m-1)2-2(4m-4)=100,
整理,得4m2-12m-91=0,
解得m=
或-
.
当m=
时,△=144-88>0,
当m=-
时,△=64+72>0,
∴m=
或-
都是原方程的根.
又当m=-
时,α+β=2m-1=-8<0,α•β=4m-4=-18,
∴α与β一正一负,这与α,β表示对角线长相矛盾.
∴m≠-
.
∴m=
.
故选A.
 解:如图.∵菱形ABCD的周长为20,
解:如图.∵菱形ABCD的周长为20,∴AB=5.
设菱形ABCD的两条对角线长分别为α,β,则α,β是方程x2-(2m-1)x+4m-4=0的两个根,
∴α+β=2m-1 ①,α•β=4m-4 ②.
∵在菱形ABCD中,AC⊥BD,AO=OC,BO=OD,
∴OA2+OB2=AB2,
即(
| α |
| 2 |
| β |
| 2 |
∴α2+β2=100,
∴(α+β)2-2αβ=100,
把①②两式分别代入,得(2m-1)2-2(4m-4)=100,
整理,得4m2-12m-91=0,
解得m=
| 13 |
| 2 |
| 7 |
| 2 |
当m=
| 13 |
| 2 |
当m=-
| 7 |
| 2 |
∴m=
| 13 |
| 2 |
| 7 |
| 2 |
又当m=-
| 7 |
| 2 |
∴α与β一正一负,这与α,β表示对角线长相矛盾.
∴m≠-
| 7 |
| 2 |
∴m=
| 13 |
| 2 |
故选A.
点评:本题主要考查了根与系数的关系,菱形的性质,一元二次方程的解法,勾股定理的应用.综合性较强,难度中等.注意运用根与系数的关系解题时,需要用判别式进行检验,此外,本题还需结合实际意义舍去不符合要求的m的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
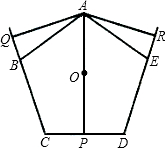 如图,ABCDE是正五边形,从顶点A向三边BC、CD、DE(或其延长线)作垂线AQ、AP、AR、(Q、P、R是垂足),O是此五边形的中心,若OP=1,求AO+AQ+AR的值.
如图,ABCDE是正五边形,从顶点A向三边BC、CD、DE(或其延长线)作垂线AQ、AP、AR、(Q、P、R是垂足),O是此五边形的中心,若OP=1,求AO+AQ+AR的值. 如图,已知边长为a的正方形ABCD,E为AD的中点,P为CE的中点,那么△BPD的面积的值是
如图,已知边长为a的正方形ABCD,E为AD的中点,P为CE的中点,那么△BPD的面积的值是