题目内容
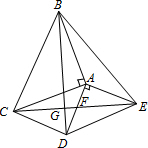 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连接BD交CE于点G,则tan∠FDG=
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连接BD交CE于点G,则tan∠FDG=考点:相似三角形的判定与性质,全等三角形的判定与性质,等腰直角三角形
专题:
分析:如图,首先证明AE=2AF,tan∠AEF=
=
;然后证明△ABD≌△ACE,得到∠FDG=∠AEF,即可解决问题.
| AF |
| AE |
| 1 |
| 2 |
解答: 解:如图,∵四边形ACDE是平行四边形,
解:如图,∵四边形ACDE是平行四边形,
∴AF=DF;而AD=AE,
∴AE=2AF,tan∠AEF=
=
;
∵∠BAC=∠EAD,
∴∠BAD=∠CAE;在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠FDG=∠AEF,
∴tan∠FDG=
.
故答案为
.
 解:如图,∵四边形ACDE是平行四边形,
解:如图,∵四边形ACDE是平行四边形,∴AF=DF;而AD=AE,
∴AE=2AF,tan∠AEF=
| AF |
| AE |
| 1 |
| 2 |
∵∠BAC=∠EAD,
∴∠BAD=∠CAE;在△ABD与△ACE中,
|
∴△ABD≌△ACE(SAS),
∴∠FDG=∠AEF,
∴tan∠FDG=
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:该题主要考查了全等三角形的判定及其性质、平行四边形的性质、三角函数的定义等知识点及其应用问题;解题的关键是牢固掌握全等三角形的判定及其性质、平行四边形的性质、三角函数的定义等知识点.

练习册系列答案
相关题目
已知一组数据:12,5,9,5,14,下列说法不正确的是( )
| A、平均数是9 | B、极差是5 |
| C、众数是5 | D、中位数是9 |
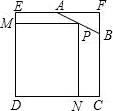 如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积.
如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积.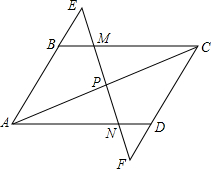 如图,在?ABCD中,EF交AB的延长线于点E,交BC于点M,交AC于点P,交AD于点N,交CD的延长线于点F.
如图,在?ABCD中,EF交AB的延长线于点E,交BC于点M,交AC于点P,交AD于点N,交CD的延长线于点F. 如图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是
如图,△ABC和△ADE均是顶角为42°的等腰三角形,BC、DE分别是底边,图中的△ABD绕A旋转42°后得到的图形是 如图中的△A′B′C′是由△ABC绕点P旋转180°后得到的图形,根据旋转的性质回答下列问题:
如图中的△A′B′C′是由△ABC绕点P旋转180°后得到的图形,根据旋转的性质回答下列问题: