题目内容
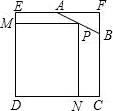 如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积.
如图,已知边长为4的正方形截取一个角后成为五边形ABCDE,其中AF=2,BF=1.P是AB边上的任一点,过P作PN⊥DC于N,PM⊥DE于M,设PN=x,矩形PNDM的面积为y,当x为何值时,矩形PNDM的面积最大,并求出最大面积.考点:二次函数的应用
专题:
分析:延长MP与CF相交于点Q,利用△BPQ与△BFA相似得到对应线段成比例,从而确定函数关系求最值即可.
解答:解: 延长MP与CF相交于点Q,
延长MP与CF相交于点Q,
∵PQ∥AF,
∴△BPQ∽△BFA,
∵PN=x,
∴PQ=2x-6,
∴CN=2x-6,
∴y=-2x2+10x,
对称轴x=2.5,
但∵3≤x≤4,
∴当x=3时,有最大面积,最大面积是-2×9+30=12.
 延长MP与CF相交于点Q,
延长MP与CF相交于点Q,∵PQ∥AF,
∴△BPQ∽△BFA,
∵PN=x,
∴PQ=2x-6,
∴CN=2x-6,
∴y=-2x2+10x,
对称轴x=2.5,
但∵3≤x≤4,
∴当x=3时,有最大面积,最大面积是-2×9+30=12.
点评:本题综合考查了二次函数的应用及相似三角形的知识,解题的关键是从实际问题中抽象出二次函数模型,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一元二次方程x2-9=0的解是( )
| A、x=-3 |
| B、x=3 |
| C、x1=3,x2=-3 |
| D、x=81 |
下列图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )
如图,△ABC和△DEF分别是⊙O的外切正三角形和内接正三角形,则它们的面积比为( )| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
 如图,有背面一样,正面分别是2、3、4、5的4张扑克牌,两次随机摸一张牌看正面的点数(每一次摸牌后放回)
如图,有背面一样,正面分别是2、3、4、5的4张扑克牌,两次随机摸一张牌看正面的点数(每一次摸牌后放回) 某文具零售店老板到批发市场选购A、B两种文具,批发价分别为12元/件,8元/件,若该店零售的A、B两种文具的日销售y(件)与零售价x(元/件)均成一次函数图象如图所示.
某文具零售店老板到批发市场选购A、B两种文具,批发价分别为12元/件,8元/件,若该店零售的A、B两种文具的日销售y(件)与零售价x(元/件)均成一次函数图象如图所示.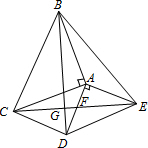 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连接BD交CE于点G,则tan∠FDG=
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连接BD交CE于点G,则tan∠FDG= 把一根绳子对折成线段AB,点A是对折点,如图从P处把绳子剪断,已知AP=
把一根绳子对折成线段AB,点A是对折点,如图从P处把绳子剪断,已知AP=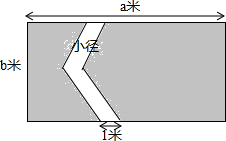 如图,某公园中有一块长a米,宽b米的长方形草坪,为方便游客穿行同时也避免草坪被随意践踏,草坪上用石子铺设了一条宽度均为1米的小径,求铺设小径后草坪(阴影部分)的面积.
如图,某公园中有一块长a米,宽b米的长方形草坪,为方便游客穿行同时也避免草坪被随意践踏,草坪上用石子铺设了一条宽度均为1米的小径,求铺设小径后草坪(阴影部分)的面积.