题目内容
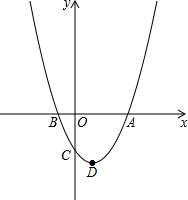 如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.
如图,已知抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),与y轴的负半轴交于点C,顶点为D.(1)直接写出抛物线的对称轴,及抛物线与x轴的另一个交点A的坐标;
(2)用只含a的代数式表示点C和点D的坐标;
(3)连结AC与CD,当AC⊥CD时.
①求抛物线的解析式;
②点E在抛物线的对称轴上,点F在抛物线上,且以B,A,F,E四点为顶点的四边形为平行四边形,求点F的坐标.
考点:二次函数综合题
专题:
分析:(1)已知抛物线解析式和点B的坐标求出a值,利用对称轴x=-
求出对称轴以及点A的坐标;
(2)设x=0,求出y的值,即点C的纵坐标,把抛物线的解析式配方即可得到顶点的坐标即点D的坐标,问题得解;
(3)①本题要靠辅助线的帮助.连接AC,AD,过DM⊥y轴于点M.证明△AOC∽△CMD后可推出a,b的值.
②证明四边形BAFE为平行四边形,求出BA,EF得出点F的坐标.
| b |
| 2a |
(2)设x=0,求出y的值,即点C的纵坐标,把抛物线的解析式配方即可得到顶点的坐标即点D的坐标,问题得解;
(3)①本题要靠辅助线的帮助.连接AC,AD,过DM⊥y轴于点M.证明△AOC∽△CMD后可推出a,b的值.
②证明四边形BAFE为平行四边形,求出BA,EF得出点F的坐标.
解答:解:(1)对称轴是直线:x=-
=-
=1,
∵抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),对称轴是直线x=1,
∴点A的坐标是(3,0);
(2)设x=0,则y=-b,
∴点C的坐标为(0,-b),
∵y=ax2-2ax-b=a(x2-2x)-b,
=a(x-1)2-a-b,
∴点D的坐标为(1,-a-b);
(3)①如图1,连接AC、AD,过D作DM⊥y轴于点M,
∵AC⊥CD,
∴∠ACD=90°,
∴∠OCA+∠MCD=90°,
∵∠OCA+∠OAC=90°,∠CDM+∠MCD=90°,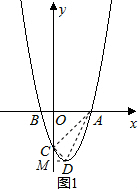
∴∠OCA=∠CDM,∠OAC=∠MCD,
∴△AOC∽△CMD,
∵点A、D、C的坐标分别是A(3,0),D(1,-a-b),C(0,-b),
∴AO=3,MD=1,
由
=
,
得
=
,
∴3-ab=0,
又∵0=a•(-1)2-2a•(-1)-b,
∴由
,
得
,
∴函数解析式为:y=x2-2x-3;
②如图2所示,当BAFE为平行四边形时,
则BA∥EF,并且BA=EF,
∵BA=4,
∴EF=4,
由于对称为x=1,
∴点F的横坐标为5,
将x=5代入y=x2-2x-3得y=12,
∴F(5,12),
根据抛物线的对称性可知,在对称轴的左侧抛物线上也存在点F,
使得四边形BAEF是平行四边形,此时点F坐标为(-3,12),
当四边形BEAF是平行四边形时,点F即为点D,
此时点F的坐标为(1,-4),
综上所述,点F的坐标为(5,12),(-3,12)或(1,-4).
| b |
| 2a |
| -2a |
| 2a |
∵抛物线y=ax2-2ax-b(a>0)与x轴的一个交点为B(-1,0),对称轴是直线x=1,
∴点A的坐标是(3,0);
(2)设x=0,则y=-b,
∴点C的坐标为(0,-b),
∵y=ax2-2ax-b=a(x2-2x)-b,
=a(x-1)2-a-b,
∴点D的坐标为(1,-a-b);
(3)①如图1,连接AC、AD,过D作DM⊥y轴于点M,
∵AC⊥CD,
∴∠ACD=90°,
∴∠OCA+∠MCD=90°,
∵∠OCA+∠OAC=90°,∠CDM+∠MCD=90°,

∴∠OCA=∠CDM,∠OAC=∠MCD,
∴△AOC∽△CMD,
∵点A、D、C的坐标分别是A(3,0),D(1,-a-b),C(0,-b),
∴AO=3,MD=1,
由
| AO |
| CM |
| OC |
| MD |
得
| 3 |
| a |
| b |
| 1 |
∴3-ab=0,
又∵0=a•(-1)2-2a•(-1)-b,
∴由
|
得
|

∴函数解析式为:y=x2-2x-3;
②如图2所示,当BAFE为平行四边形时,
则BA∥EF,并且BA=EF,
∵BA=4,
∴EF=4,
由于对称为x=1,
∴点F的横坐标为5,
将x=5代入y=x2-2x-3得y=12,
∴F(5,12),
根据抛物线的对称性可知,在对称轴的左侧抛物线上也存在点F,
使得四边形BAEF是平行四边形,此时点F坐标为(-3,12),
当四边形BEAF是平行四边形时,点F即为点D,
此时点F的坐标为(1,-4),
综上所述,点F的坐标为(5,12),(-3,12)或(1,-4).
点评:本题考查的是二次函数的综合运用以及平行四边形的判定定理,利用数形结合以及分类讨论得出F点的坐标是解题关键,题目的综合性较强,对学生的解题能力要求较高,是一道不错的中考题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,∠BAC=30°,点D是BC边上的点,CD=
如图,在Rt△ABC中,∠C=90°,∠BAC=30°,点D是BC边上的点,CD=| 3 |
A、2
| ||
B、
| ||
C、
| ||
| D、4 |
甲乙两人同时同地同向出发沿400米环形跑道跑步,甲的速度比乙快,当甲第二次追上乙时,甲比乙跑的路程( )
| A、一样多 | B、多800m |
| C、多400m | D、少400m |
 如图,在直角形坐标系中有两点A(6,0)、B(0,8),点C为AB的中点,点D在x轴上,当点D的坐标为
如图,在直角形坐标系中有两点A(6,0)、B(0,8),点C为AB的中点,点D在x轴上,当点D的坐标为 根据二次函数y=x2+3x-4的图象回答:
根据二次函数y=x2+3x-4的图象回答:
 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF. 小红在做作业时,不小心将墨水洒在一条数轴上,如图所示,根据图中标出的数值,判断墨迹盖住的整数共有
小红在做作业时,不小心将墨水洒在一条数轴上,如图所示,根据图中标出的数值,判断墨迹盖住的整数共有