Question

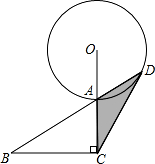
如图，已知在R△ABC中，∠B=30°，∠ACB=90°，延长CA到O，使AO=AC，以O为圆心，OA长为半径作⊙O交BA延长线于点D，连接CD．

（1）求证：CD是⊙O的切线；

（2）若AB=4，求图中阴影部分的面积．

Answer 1

（1）证明：连接OD，

∵∠BCA=90°，∠B=30°，

∴∠OAD=∠BAAC=60°，

∵OD=OA，

∴△OAD是等边三角形，

∴AD=OA=AC，∠ODA=∠O=60°，

∴∠ADC=∠ACD=∠OAD=30°，

∴∠ODC=60°+30°=90°，

即OD⊥DC，

∵OD为半径，

∴CD是⊙O的切线；

（2）解：∵AB=4，∠ACB=90°，∠B=30°，

∴OD=OA=AC=AB=2，

由勾股定理得：CD===2，

∴S_阴影=S_△ODC﹣S_扇形AOD=×2×2﹣=2﹣π．