题目内容
18.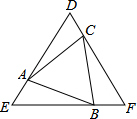 已知:如图,在等边三角形ABC中,过点A、B、C分别作AB、BC、AC的垂线,两两相交于点D、E、F.求证:△DEF是等边三角形.
已知:如图,在等边三角形ABC中,过点A、B、C分别作AB、BC、AC的垂线,两两相交于点D、E、F.求证:△DEF是等边三角形.
分析 根据等边三角形的性质得到AB=BC=AC,∠CAB=∠ACB=∠ABC=60°,由垂直的定义得到∠EAB=∠CBF=∠ACD=∠DAB=∠EBC=∠ACF=90°,于是得到∠DAC=∠ABE=∠BCF=30°,推出∠D=∠E=∠F=60°,于是得到结论.
解答 解:在等边三角形ABC中,
∵AB=BC=AC,∠CAB=∠ACB=∠ABC=60°,
∵过点A、B、C分别作AB、BC、AC的垂线,
∴∠EAB=∠CBF=∠ACD=∠DAB=∠EBC=∠ACF=90°,
∴∠DAC=∠ABE=∠BCF=30°,
∴∠D=∠E=∠F=60°,
∴△DEF是等边三角形.
点评 本题考查了等边三角形的判定和性质,垂直的定义,三角形的内角和,熟练掌握等边三角形的判定和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9. 如图,将三角尺的直角顶点放在直尺的一边上,∠1=20°,∠2=50°,则∠3的度数是( )
如图,将三角尺的直角顶点放在直尺的一边上,∠1=20°,∠2=50°,则∠3的度数是( )
 如图,将三角尺的直角顶点放在直尺的一边上,∠1=20°,∠2=50°,则∠3的度数是( )
如图,将三角尺的直角顶点放在直尺的一边上,∠1=20°,∠2=50°,则∠3的度数是( )| A. | 50° | B. | 30° | C. | 20° | D. | 15° |
 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD折叠后,点C落在E处,连接BE,若BE=4,则BC长=4$\sqrt{2}$.
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD折叠后,点C落在E处,连接BE,若BE=4,则BC长=4$\sqrt{2}$. 如图,将长为10cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形=6cm2.
如图,将长为10cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形=6cm2. 如图,请画出一个图形经过两次轴对称变换之后得到的图形,其中图①中的两条对称轴是平行的,图②中的两条对称轴是垂直的.仔细观察上面的两个图形经过两次轴对称变换之后得到的图形.图①中的图形除经过两次轴对称变换得到之外,还可以通过我们学过的平移变换得到,图②中的图形还可以通过旋转变换得到.
如图,请画出一个图形经过两次轴对称变换之后得到的图形,其中图①中的两条对称轴是平行的,图②中的两条对称轴是垂直的.仔细观察上面的两个图形经过两次轴对称变换之后得到的图形.图①中的图形除经过两次轴对称变换得到之外,还可以通过我们学过的平移变换得到,图②中的图形还可以通过旋转变换得到.