题目内容
6. 如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD折叠后,点C落在E处,连接BE,若BE=4,则BC长=4$\sqrt{2}$.
如图,AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD折叠后,点C落在E处,连接BE,若BE=4,则BC长=4$\sqrt{2}$.
分析 根据题意可知DE为BC的垂直平分线,由翻折的性质可知:CD=DE,故此BD=DE,在Rt△BDE中,利用特殊锐角三角函数值可求得BD的长,然后可求得BC的长.
解答 解:∵AD是△ABC的中线,
∴BD=CD.
由翻折的性质可知:∠EDA=∠ADC=45°,CD=DE.
∴∠BDE=90°,BD=DE.
∴BD=sin45°BE=$\frac{\sqrt{2}}{2}×4$=2$\sqrt{2}$.
∴BC=2BD=2×2$\sqrt{2}$=4$\sqrt{2}$.
故答案为:4$\sqrt{2}$.
点评 本题主要考查的是翻折的性质、证得△BDE为等腰直角三角形的是解题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,直线y=x+4与抛物线y=ax2-3x+c交于A、B两点,点A在x轴上,点B在y轴上.
如图,在平面直角坐标系中,直线y=x+4与抛物线y=ax2-3x+c交于A、B两点,点A在x轴上,点B在y轴上. 如图,正方形OABC的各顶点A、B、C的坐标如图,则点B坐标是(2,2),点C的坐标是(2,0).
如图,正方形OABC的各顶点A、B、C的坐标如图,则点B坐标是(2,2),点C的坐标是(2,0). 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,若BC=3,sin∠BPD=$\frac{3}{5}$,则⊙O的直径为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,若BC=3,sin∠BPD=$\frac{3}{5}$,则⊙O的直径为( ) 平面上有△ACD与△BCE,其中AD与BE相交于P点,若AC=BC,CD=CE,∠ACB=∠ECD.
平面上有△ACD与△BCE,其中AD与BE相交于P点,若AC=BC,CD=CE,∠ACB=∠ECD. 已知线段AB,如图所示,在线段AB上求作一点P,使AP:PB=2:3(保留作图痕迹.不写作法).
已知线段AB,如图所示,在线段AB上求作一点P,使AP:PB=2:3(保留作图痕迹.不写作法).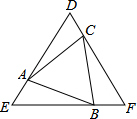 已知:如图,在等边三角形ABC中,过点A、B、C分别作AB、BC、AC的垂线,两两相交于点D、E、F.求证:△DEF是等边三角形.
已知:如图,在等边三角形ABC中,过点A、B、C分别作AB、BC、AC的垂线,两两相交于点D、E、F.求证:△DEF是等边三角形.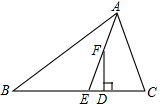 如图,在△ABC中,AE平分∠BAC,F为AE上一点,且FD⊥BC于点D,若∠C-∠B=40°,求∠EFD的度数.
如图,在△ABC中,AE平分∠BAC,F为AE上一点,且FD⊥BC于点D,若∠C-∠B=40°,求∠EFD的度数.