题目内容
10.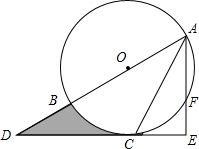 如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
分析 (1)连接OC,先证明∠OAC=∠OCA,进而得到OC∥AE,于是得到OC⊥CD,进而证明DE是⊙O的切线;
(2)分别求出△OCD的面积和扇形OBC的面积,利用S阴影=S△COD-S扇形OBC即可得到答案.
解答 (1)证明:连接OC,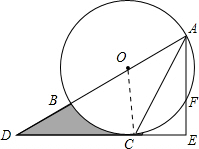
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠BAE,
∴∠OAC=∠CAE,
∴∠OCA=∠CAE,
∴OC∥AE,
∴∠OCD=∠E,
∵AE⊥DE,
∴∠E=90°,
∴∠OCD=90°,
∴OC⊥CD,
∵点C在圆O上,OC为圆O的半径,
∴CD是圆O的切线;
(2)解:在Rt△AED中,
∵∠D=30°,AE=6,
∴AD=2AE=12,
在Rt△OCD中,∵∠D=30°,
∴DO=2OC=DB+OB=DB+OC,
∴DB=OB=OC=$\frac{1}{3}$AD=4,DO=8,
∴CD=$\sqrt{D{O}^{2}-O{C}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴S△OCD=$\frac{CD•OC}{2}$=$\frac{4\sqrt{3}×4}{2}$=8$\sqrt{3}$,
∵∠D=30°,∠OCD=90°,
∴∠DOC=60°,
∴S扇形OBC=$\frac{1}{6}$×π×OC2=$\frac{8}{3}π$,
∵S阴影=S△COD-S扇形OBC
∴S阴影=8$\sqrt{3}$-$\frac{8π}{3}$,
∴阴影部分的面积为8$\sqrt{3}$-$\frac{8π}{3}$.
点评 本题主要考查了切线的判定以及扇形的面积计算,解(1)的关键是证明OC⊥DE,解(2)的关键是求出扇形OBC的面积,此题难度一般.

练习册系列答案
相关题目
1.120°的圆心角对的弧长是6π,则此弧所在圆的半径是( )
| A. | 3 | B. | 4 | C. | 9 | D. | 18 |
5.据《云南省生物物种名录(2016版)的》介绍,在素有“动植物王国”之美称的云南,已经发现的动植物有25434种,25434用科学记数法表示为( )
| A. | 2.5434×103 | B. | 2.5434×104 | C. | 2.5434×10-3 | D. | 2.5434×10-4 |
15.如表是我市4个区县今年5月31日最高气温(℃)的统计结果:
该日最高气温的众数和中位数分别是( )
| 永定区 | 武陵源区 | 慈利县 | 桑植县 |
| 32 | 32 | 33 | 30 |
| A. | 32℃,32℃ | B. | 32℃,33℃ | C. | 33℃,33℃ | D. | 32℃,30℃ |
15.反比例函数y=-$\frac{3}{x}$的图象上有P1(x1,-2),P2(x2,-3)两点,则x1与x2的大小关系是( )
| A. | x1>x2 | B. | x1=x2 | C. | x1<x2 | D. | 不确定 |
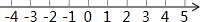 求不等式组$\left\{\begin{array}{l}5x-3<4x\\ 4(x+1)+2≥x\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.
求不等式组$\left\{\begin{array}{l}5x-3<4x\\ 4(x+1)+2≥x\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.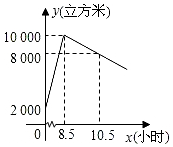 星期天8:00~8:30,燃气公司给加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.
星期天8:00~8:30,燃气公司给加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.