已知$\frac{x}{3}=\frac{y}{4}=\frac{z}{5}$.则$\frac{x+y+z}{x}$=4．题目和参考答案——青夏教育精英家教网—

题目内容

18．已知$\frac{x}{3}=\frac{y}{4}=\frac{z}{5}$，则$\frac{x+y+z}{x}$=4．

分析根据等式的性质，可用k表示x、y、z，根据分式的性质，可得答案．

解答解：由$\frac{x}{3}=\frac{y}{4}=\frac{z}{5}$，得
x=3k，y=4k，z=5k．
$\frac{x+y+z}{x}$=$\frac{3k+4k+5k}{3k}$=4，
故答案为：4．

点评本题考查了比例的性质，利用等式的性质得出x=3k，y=4k，z=5k是解题关键．

练习册系列答案

相关题目

8．

如图，Rt△ABC中∠A=90°，∠C=30°，BD平分∠ABC且与AC边交于点D，AD=2，则点D到边BC的距离是2．

9．2016年1月5日，河北外国语学院举行“我说我校训”大学生演讲比赛，参赛选手共有12名．梦梦根据比赛中七位评委所给的某位参赛选手的分数制作了如下表格，如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是（　　）

众数	中位数	平均数	方差
9.2	9.1	9.1	0.2

6．

如图，四边形OABC是菱形，对角线OB在x轴负半轴上，位于第二象限的点A和第三象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上，分别过点A、C作y轴的垂线，垂足分别为E和F．下列结论：①|k₁|=|k₂|；②AE=CF；③若四边形OABC是正方形，则∠EAO=45°．其中正确的有（　　）

13．

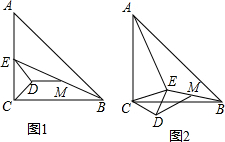如图1，△ABC和△CDE都是等腰直角三角形，∠ACB=∠CDE=90°，点E在AC上，M为BE的中点
（1）求证：AE=2DM；
（2）将图1中的△CDE旋转至图2的位置，试探究AE与DM之间的等量关系．

3．点（1，y₁），（-2，y₂），（3，y₃）均在函数$y=\frac{6}{x}$的图象上，则y₁，y₂，y₃的大小关系是y₁＞y₃＞y₂．

10．

如图，∠AOC=∠BOD=90°，图中相等的角是∠AOB=∠COD，依据是同角的余角相等．

7．先化简，再求值：$\frac{{{x^2}-4x+4}}{{{x^2}-2x}}÷（x-\frac{4}{x}）$，其中x=-1．

8．

如图，正方形PQMN的边PQ在x轴上，点M坐标为（2，1），将正方形PQMN沿x轴连续翻转，则经过点（2015，$\sqrt{2}$）的顶点是（　　）

试题分类