题目内容
6. 如图,四边形OABC是菱形,对角线OB在x轴负半轴上,位于第二象限的点A和第三象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A、C作y轴的垂线,垂足分别为E和F.下列结论:①|k1|=|k2|;②AE=CF;③若四边形OABC是正方形,则∠EAO=45°.其中正确的有( )
如图,四边形OABC是菱形,对角线OB在x轴负半轴上,位于第二象限的点A和第三象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A、C作y轴的垂线,垂足分别为E和F.下列结论:①|k1|=|k2|;②AE=CF;③若四边形OABC是正方形,则∠EAO=45°.其中正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 连接AC交OB于D,由菱形的性质得出AC⊥OB,AD=CD,BD=OD,得出△AOD的面积=△COD的面积,由三角形的面积与k的关系即可得出①正确;
证出四边形ADOE是矩形,得出AE=DO,同理:CF=DO,得出AE=CF,②正确;
若四边形OABC是正方形,则∠AOB=45°,得出∠AOE=45°,求出∠EAO=45°,③正确;即可得出结论.
解答 解:连接AC交OB于D,如图所示: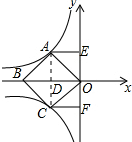
∵四边形OABC是菱形,
∴AC⊥OB,AD=CD,BD=OD,
∴△AOD的面积=△COD的面积,
∵△AOD的面积=$\frac{1}{2}$|k1|,△COD的面积=$\frac{1}{2}$|k2|,
∴|k1|=|k2|,①正确;
∵AE⊥y轴,AC⊥BD,
∴∠AEO=∠ADO=90°,
∵∠DOE=90°,
∴四边形ADOE是矩形,
∴AE=DO,
同理:CF=DO,
∴AE=CF,②正确;
若四边形OABC是正方形,则∠AOB=45°,
∴∠AOE=90°-45°=45°,
∵∠AEO=90°,
∴∠EAO=45°,③正确;
正确的有3个,故选:D.
点评 本题是反比例函数的综合题,考查了反比例函数的图象、反比例函数k的几何意义、菱形的性质、矩形的判定与性质以及正方形的性质;熟练掌握菱形的对角线互相垂直平分的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列各数中,最小的数是( )
| A. | 1 | B. | -|-2| | C. | $\sqrt{3}$ | D. | 2×10-10 |
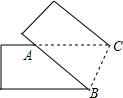 将一张宽为4cm的矩形纸片折叠成如图所示图形,若AB=6cm,则AC的长度为6cm.
将一张宽为4cm的矩形纸片折叠成如图所示图形,若AB=6cm,则AC的长度为6cm.
 如图是由6个相同的小立方块搭成的几何体,那么这个几何体的左视图是( )
如图是由6个相同的小立方块搭成的几何体,那么这个几何体的左视图是( )


