题目内容
13.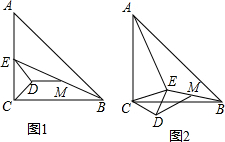 如图1,△ABC和△CDE都是等腰直角三角形,∠ACB=∠CDE=90°,点E在AC上,M为BE的中点
如图1,△ABC和△CDE都是等腰直角三角形,∠ACB=∠CDE=90°,点E在AC上,M为BE的中点(1)求证:AE=2DM;
(2)将图1中的△CDE旋转至图2的位置,试探究AE与DM之间的等量关系.
分析 (1)如图1,延长ED交BC于N,根据等腰直角三角形的性质得到AC=BC,DE=CD,推出△ECN是等腰直角三角形,得到CE=CN,求得AE=BN,根据三角形的中位线的性质到DM=$\frac{1}{2}$BN,等量代换得到结论;
(2)如图2,延长ED到N使DN=DE,推出△CEN是等腰直角三角形,得到∠ACE=∠BCN,通过△ACE≌△BCN,得到AE=BN,于是得到结论.
解答 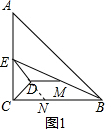 解:(1)如图1,延长ED交BC于N,
解:(1)如图1,延长ED交BC于N,
∵△ABC和△CDE都是等腰直角三角形,
∴AC=BC,DE=CD,
∵∠ACB=90°,∠ECD=45°,
∴∠CDN=90°,∠DCN=45°,
∴△ECN是等腰直角三角形,
∴CE=CN,
∴AC-CE=BC-CN,
即AE=BN,
∵EM=BM,
∴DM=$\frac{1}{2}$BN,
∴AE=2DM;
(2)AE=2DM ,如图2,延长ED到N使DN=DE,
,如图2,延长ED到N使DN=DE,
∵∠CDN=90°,
∴CD⊥EN,
∴CN=CE,
∴△CEN是等腰直角三角形,
∴∠ECD=90°,
∴∠ACE=∠BCN,
在△ACE与△BCN中,$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCN}\\{CE=CN}\end{array}\right.$,
∴△ACE≌△BCN,
∴AE=BN,
∵BM=EM,
∴DM=$\frac{1}{2}$BN,
∴AE=2DM.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,三角形的中位线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
3.云南省鲁甸县2014年8月3日发生6.5级地震,造成重大人员伤亡和经济损失.灾情牵动亿万同胞的心,在灾区人民最需要援助的时刻,全国同胞充分发扬“一方有难、八方支援”的中华民族优良传统,及时向灾区同胞伸出援助之手.截至9月19日17时,云南省级共接收昭通鲁甸“8.3”地震捐款80100万元.科学记数法表示为( )元.
| A. | 8.01×107 | B. | 80.1×107 | C. | 8.01×108 | D. | 0.801×109 |
1.下列各数中,最小的数是( )
| A. | 1 | B. | -|-2| | C. | $\sqrt{3}$ | D. | 2×10-10 |
5.一组数据如下:3,6,7,2,3,4,3,6,那么这组数据的中位数和众数分别是( )
| A. | 3,3 | B. | 3.5,3 | C. | 4,3 | D. | 3.5,6 |
 请你根据王老师所给的内容,完成下列各小题.
请你根据王老师所给的内容,完成下列各小题.