题目内容
2. 如图,AB∥DE,∠1=∠2=60°,B、E、C在同一条直线上,∠CED=2∠AEB,求∠C的度数.
如图,AB∥DE,∠1=∠2=60°,B、E、C在同一条直线上,∠CED=2∠AEB,求∠C的度数.
分析 根据AB∥DE,得∠1=∠AED,再由∠CED=2∠AEB,设∠AEB=x,则∠CED=2x,再列出关于x的方程,求出∠C的度数即可.
解答 解:∵AB∥DE,
∴∠1=∠AED,
∵∠1=∠2=60°,
∴∠AED=60°,
∴AE∥CD,
∴∠C=∠AEB,
∵∠CED=2∠AEB,设∠AEB=x,则∠CED=2x,
∴x+2x+60=180°,
∴x=40°,
∴∠C=40,
∴∠C的度数为40°.
点评 本题利用了平行线的性质:两直线平行,内错角相等;两直线平行,同旁内角互补.

练习册系列答案
相关题目
13. 如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
 如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
10.下列说法:
①对顶角相等;
②过直线外一点有且只有一条直线与这条直线平行;
③直线外一点与直线上各点连接的所有线段中,垂线段最短;
④一个角的余角比它的补角大90°.
其中正确的个数为( )
①对顶角相等;
②过直线外一点有且只有一条直线与这条直线平行;
③直线外一点与直线上各点连接的所有线段中,垂线段最短;
④一个角的余角比它的补角大90°.
其中正确的个数为( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
7.下列说法正确的是( )
| A. | 为了解2016年春节联欢晚会收视情况,应采用全面调查方式 | |
| B. | 为了解全国中学生的视力状况,应采用普查方式 | |
| C. | 乘坐高铁时,检查旅客行李是否携带有违禁物品应采用抽样调查方式 | |
| D. | 为了解2016年春节中国人最喜欢的过年方式应采用抽样调查方式 |
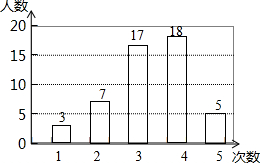 某校为了解全校1500名学生参加社会实践活动的情况,随机调查了50名学生每人参加社会实践活动的次数,并根据数据绘成条形统计图如下:
某校为了解全校1500名学生参加社会实践活动的情况,随机调查了50名学生每人参加社会实践活动的次数,并根据数据绘成条形统计图如下: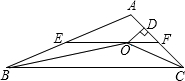 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①∠BOC=90°+$\frac{1}{2}∠A$;②EF=BE+CF;③设OD=m,AE:AF=n,则S△AEF=$\frac{1}{2}mn$;④EF是△ABC的中位线.其中正确的结论是 ( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①∠BOC=90°+$\frac{1}{2}∠A$;②EF=BE+CF;③设OD=m,AE:AF=n,则S△AEF=$\frac{1}{2}mn$;④EF是△ABC的中位线.其中正确的结论是 ( ) 如图,点A、C、B、D在⊙O上,∠AOB=60°,OC平分∠AOB,则∠CDB的度数是15°.
如图,点A、C、B、D在⊙O上,∠AOB=60°,OC平分∠AOB,则∠CDB的度数是15°. 如图,∠A=90°,∠ABC的角平分线交AC于E,AE=3,则E到BC的距离为3.
如图,∠A=90°,∠ABC的角平分线交AC于E,AE=3,则E到BC的距离为3.