题目内容
6.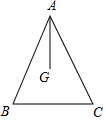 如图,G为△ABC的重心,如果AB=AC=13,BC=10,那么AG的长为8.
如图,G为△ABC的重心,如果AB=AC=13,BC=10,那么AG的长为8.
分析 延长AG交BC于D,根据重心的概念得到∠BAD=∠CAD,根据等腰三角形的性质求出BD,根据勾股定理和重心的性质计算即可.
解答 解: 延长AG交BC于D,
延长AG交BC于D,
∵G为△ABC的重心,
∴∠BAD=∠CAD,
∵AB=AC,
∴BD=$\frac{1}{2}$BC=5,AD⊥BC,
由勾股定理得,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=12,
∵G为△ABC的重心,
∴AG=$\frac{2}{3}$AD=8,
故答案为:8.
点评 本题考查的是三角形的重心的概念和性质,掌握重心到顶点的距离与重心到对边中点的距离之比为2:1是解题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
1.已知非零向量$\overrightarrow{a}$、$\overrightarrow{b}$之间满足$\overrightarrow{a}$=-3$\overrightarrow{b}$,下列判断正确的是( )
| A. | $\overrightarrow a$的模为3 | B. | $\overrightarrow a$与$\overrightarrow b$的模之比为-3:1 | ||
| C. | $\overrightarrow a$与$\overrightarrow b$平行且方向相同 | D. | $\overrightarrow a$与$\overrightarrow b$平行且方向相反 |
18.下列抛物线中,顶点坐标是(-2,0)的是( )
| A. | y=x2+2 | B. | y=x2-2 | C. | y=(x+2)2 | D. | y=(x-2)2 |
15.将二次函数y=2x2-1的图象向下平移3个单位后所得图象的函数解析式为( )
| A. | y=2(x-3)2-1 | B. | y=2(x+3)2-1 | C. | y=2x2+4 | D. | y=2x2-4 |
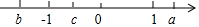 有理数a,b,c在数轴上的位置如图所示,且|a|=|b|
有理数a,b,c在数轴上的位置如图所示,且|a|=|b|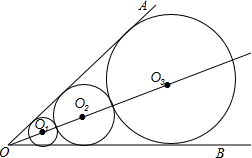 如图所示,已知∠AOB=60°,☉O1与∠AOB的两边都相切,沿OO1方向做☉O2与∠AOB的两边相切,且与☉O1外切,再作☉O3与∠AOB的两边相切,且与☉O2外切,…,如此作下去,☉On与∠AOB的两边相切,且与☉On-1外切,设☉On的半径为rn,已知r1=1则r2016=32015.
如图所示,已知∠AOB=60°,☉O1与∠AOB的两边都相切,沿OO1方向做☉O2与∠AOB的两边相切,且与☉O1外切,再作☉O3与∠AOB的两边相切,且与☉O2外切,…,如此作下去,☉On与∠AOB的两边相切,且与☉On-1外切,设☉On的半径为rn,已知r1=1则r2016=32015.