题目内容
18.已知$\root{3}{2-x}$+x=2,且$\root{3}{2y-1}$与$\root{3}{1-3x}$互为相反数,求x、y的值.分析 利用立方根的意义,求出x,然后用相反数的意义,求出y.
解答 解:∵$\root{3}{2-x}+x=2$,
∴$\root{3}{2-x}=2-x$
∴2-x=(2-x)3
∴(2-x)2=1
∴x=1或x=3,
∵$\root{3}{2y-1}$与$\root{3}{1-3x}$互为相反数,
∴$\root{3}{2y-1}+\root{3}{1-3x}=0$,
∴$\root{3}{2y-1}=-\root{3}{1-3x}$.
当x=1时,$\root{3}{2y-1}=-\root{3}{-2}=\root{3}{2}$;
∴2y-1=2,即:y=$\frac{3}{2}$.
当x=3时,$\root{3}{2y-1}=-\root{3}{-8}=\root{3}{8}$;
∴2y-1=8,即:y=$\frac{9}{2}$.
点评 本题是一道用到多个知识点(如:直接开平方解简单的一元二次方程,立方根的性质,如果$\root{3}{a}=\root{3}{b}$,那么a=b)的中等试题,主要考查立方根的意义和相反数的性质.

练习册系列答案
相关题目
10.小明从家出发,先向东走350m到小亮家,然后它们又向南走500m到老师家,如果以老师家的位置为平面直角坐标系的坐标原点,正东方向为x轴正方向为x轴正方向,正北方向为y轴正方向,那么小明家的位置可记为( )
| A. | (350,500) | B. | (-350,-500) | C. | (350,-500) | D. | (-350,500) |
7.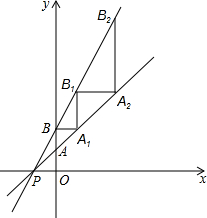 如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
 如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )| A. | (63,64) | B. | (65,64) | C. | (31,32) | D. | (127,128) |
 如图所示,将一个矩形ABCD纸片,剪去两个完全相同的矩形后,剩余的阴影部分纸片面积大小为24,且AB=8,则被剪掉的矩形的长为6.
如图所示,将一个矩形ABCD纸片,剪去两个完全相同的矩形后,剩余的阴影部分纸片面积大小为24,且AB=8,则被剪掉的矩形的长为6.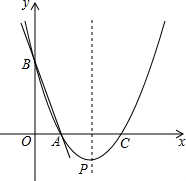 如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.
如图,直线y=-3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x-2)2+k经过点A、B,并与x轴交于另一点C,其顶点为P.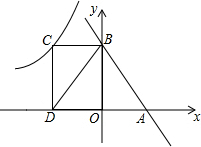 如图,直线y=-x+2与x轴、y轴分别交于A、B两点,过B点作BC⊥y轴与双曲线y=$\frac{k}{x}$(k<0)交于C点,过C作CD⊥x轴于D.若△BOD的面积为3,则k的值为-6.
如图,直线y=-x+2与x轴、y轴分别交于A、B两点,过B点作BC⊥y轴与双曲线y=$\frac{k}{x}$(k<0)交于C点,过C作CD⊥x轴于D.若△BOD的面积为3,则k的值为-6.