题目内容
计算:(2+1)(2-1)(24+1)(28+1)(216+1)+1.
考点:平方差公式
专题:计算题
分析:原式利用平方差公式计算即可得到结果.
解答:解:原式=
(22-1)(22+1)(24+1)(28+1)(216+1)+1
=
(24-1)(24+1)(28+1)(216+1)+1
=
(28-1)(28+1)(216+1)+1
=
(216-1)(216+1)+1
=
(232-1)+1
=
×232+
.
| 1 |
| 5 |
=
| 1 |
| 5 |
=
| 1 |
| 5 |
=
| 1 |
| 5 |
=
| 1 |
| 5 |
=
| 1 |
| 5 |
| 4 |
| 5 |
点评:此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下列运算错误的是( )
| A、(-a)(-a)2=(-a)3 |
| B、-32•(-3)4=(-3)6 |
| C、(-a)2•(-a)3=(-a)5 |
| D、(-a)3•(-a)3=a6 |
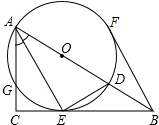 如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于E,点O在AB上,以OA为半径的圆,交AB于D,交AC于C,且点E在⊙O上,连接DE,BF切⊙O于点F.
如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于E,点O在AB上,以OA为半径的圆,交AB于D,交AC于C,且点E在⊙O上,连接DE,BF切⊙O于点F.