题目内容
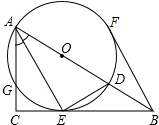 如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于E,点O在AB上,以OA为半径的圆,交AB于D,交AC于C,且点E在⊙O上,连接DE,BF切⊙O于点F.
如图,在△ABC中,∠C=90°,AE平分∠BAC交BC于E,点O在AB上,以OA为半径的圆,交AB于D,交AC于C,且点E在⊙O上,连接DE,BF切⊙O于点F.(1)求证:BE=BF;
(2)若⊙O的半径为R,AG=R+1,CE=R-1,求弦AG的长.
考点:切线的性质
专题:
分析:(1)连接OE,证出OE⊥CD,再由切线长定理易得BE=BF;
(2)根据直径所对的圆周角得出∠AGD=90°,从而证得GD∥BC,进而证得OE⊥GD,根据垂径定理得出GH=DH,然后证得四边形GCEH是矩形,从而证得GD=2(R-1)=2R-2,最后根据勾股定理求得R,即可求得AG的长.
(2)根据直径所对的圆周角得出∠AGD=90°,从而证得GD∥BC,进而证得OE⊥GD,根据垂径定理得出GH=DH,然后证得四边形GCEH是矩形,从而证得GD=2(R-1)=2R-2,最后根据勾股定理求得R,即可求得AG的长.
解答:(1)证明:连接DG、OE,交于点H.
∵AE平分∠BAC交BC于E,
∴∠CAE=∠DAE,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠CAE=∠OEA,
∴AC∥OE,
∴∠OEB=∠C=90°,
∴OE⊥BC,
∴BC是圆的切线,
∴BE=BF;
(2)解:∵AB是直径,
∵∠AGD=90°,
∵∠C=90°,
∴GD∥BC,
∵OE⊥BC,
∴OE⊥GD,
∴GH=DH,
∵∠AGD=90°,∠C=90°,OE⊥BC,
∴四边形GCEH是矩形,
∴GH=CE=R-1,
∴GD=2(R-1)=2R-2,
在直角三角形AGD中,AG2+GD2=AD2,
即(R+1)2+(2R-2)2=(2R)2
解得R1=5,R2=1(舍去),
∴AG=R+1=5+1=6;
∵AE平分∠BAC交BC于E,
∴∠CAE=∠DAE,
∵OA=OE,
∴∠OAE=∠OEA,

∴∠CAE=∠OEA,
∴AC∥OE,
∴∠OEB=∠C=90°,
∴OE⊥BC,
∴BC是圆的切线,
∴BE=BF;
(2)解:∵AB是直径,
∵∠AGD=90°,
∵∠C=90°,
∴GD∥BC,
∵OE⊥BC,
∴OE⊥GD,
∴GH=DH,
∵∠AGD=90°,∠C=90°,OE⊥BC,
∴四边形GCEH是矩形,
∴GH=CE=R-1,
∴GD=2(R-1)=2R-2,
在直角三角形AGD中,AG2+GD2=AD2,
即(R+1)2+(2R-2)2=(2R)2
解得R1=5,R2=1(舍去),
∴AG=R+1=5+1=6;
点评:此题考查的知识点是切线的判定、平行线的判定与性质、矩形的判定和性质以及勾股定理的应用,解题的关键是添加辅助线构造直角三角形.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
如果用+3吨表示运入仓库3吨大米,那么从仓库运出4吨大米可以表示为( )
| A、-4吨 | B、+4吨 |
| C、-3吨 | D、+3吨 |
 如图,在等边△ABC中,AD=BE=CF,D、E、F不是中点,连结AE、CD,构成一些三角形.如果三个全等三角形的三角形组成一组,那么图中全等的三角形的组数是( )
如图,在等边△ABC中,AD=BE=CF,D、E、F不是中点,连结AE、CD,构成一些三角形.如果三个全等三角形的三角形组成一组,那么图中全等的三角形的组数是( )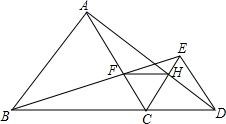 如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,