Question

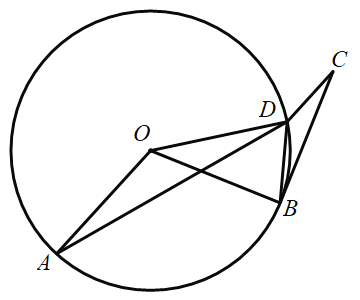
【题目】如图，点A、点D为⊙O上两点，线段BC切⊙O于点B，点D在BC的垂直平分线上，CD∥OA，sin∠BCD=，OA=2BD，若BC=，则⊙O的半径为（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】

过点D作DE⊥BC于点E，由点D在BC的垂直平分线上，可知E为BC的中点，BD=DC，再由sin∠BCD=可设DE=2x，CE=5x.再根据勾股定理列出方程求出x的值，再根据OA=2BD=2CD,求出OA的值.

解：如图，过点D作DE⊥BC于点E，则

∵点D在BC的垂直平分线上，

∴E为BC的中点，BD=DC，

∵BC=，

∴CE= .

∵sin∠BCD=，

∴设DE=2x，CE=5x.

在Rt△CDE中，

解得，x= .

.

∴OA=2BD=2DC=.

故选A.