题目内容
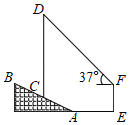
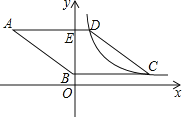
【题目】如图,△DEF由△ABC平移得到,∠DFE=∠CDF=30°,∠DEF=90°,BE⊥DF于点B.连接CE,AB=3.
(1)求证:四边形ACDF为矩形
(2)求线段CE的长和△CEF的面积.
【答案】(1)证明见解析;(2)CE=![]() ,S△CEF=
,S△CEF=![]()
【解析】
(1)先证明四边形ACFD为平行四边形,再结合∠CFD=90°得到结论;
(2)作EG⊥CF的延长线于点G,利用矩形的性质证明四边形ABED为平行四边形,从而证明四边形BEGF为矩形,得到FG=BE,EG=BF,利用三角形面积得到BE,再利用勾股定理得到CG和EG,从而算出CE,最后利用S△CEF=![]() 算出结果.
算出结果.
解:(1)证明:∵△DEF由△ABC平移得到
∴DF∥AC,即四边形ACFD为平行四边形
∵CF⊥DF,
∴∠CFD=90°,
∴平行四边形ACDF为矩形;
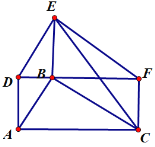
(2)如图所示:作EG⊥CF的延长线于点G.
∵△DEF由△ABC平移得到,四边形ACDF为矩形,
∴DE∥AB,
即四边形ABED为平行四边形,
∵DF经过点B.
∴∠ADF=∠DBE=90°,AD∥BE
同理可得∠CFB=∠FBE=90°,CF∥BE
∵∠CFB+∠EBF=180°,EG⊥CF
∴∠EBF=∠FBE=∠EGF=90°
∴四边形BEGF为矩形,FG=BE,EG=BF
∵∠DFE=∠CDF=30°,∠DEF=90°
∴DF=2DE=6,
在Rt△DEF中:EF=![]() =
=![]()
∵S△DEF=![]() =
=![]()
∴BE=![]() =
=![]() ,
,
在Rt△BEF中:BF=![]() =
=![]() ,
,
∴CG=CF+FG=2BE=![]() ,EG=
,EG=![]() ,
,
∴在Rt△CEG中:CE=![]()
∴S△CEF=![]() =
=![]() .
.


 阅读快车系列答案
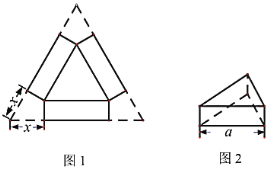
阅读快车系列答案【题目】如图1,小明用一张边长为![]() 的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为
的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为![]() ,再折成如图2所示的无盖糖果盒,它的容积记为
,再折成如图2所示的无盖糖果盒,它的容积记为![]() .
.
(1)![]() 关于
关于![]() 的函数关系式是__________,自变量
的函数关系式是__________,自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)为探究![]() 随
随![]() 的变化规律,小明类比二次函数进行了如下探究:
的变化规律,小明类比二次函数进行了如下探究:
①列表:请你补充表格中的数据:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| 0 | 3.125 | ________ | 3.375 | ________ | 0.625 | 0 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:请你用光滑的曲线顺次连接各点.

(3)利用函数图象解决:
①该糖果盒的最大容积是__________;
②若该糖果盒的容积超过![]() ,请估计糖果盒的底边长
,请估计糖果盒的底边长![]() 的取值范围.(保留一位小数)
的取值范围.(保留一位小数)