题目内容
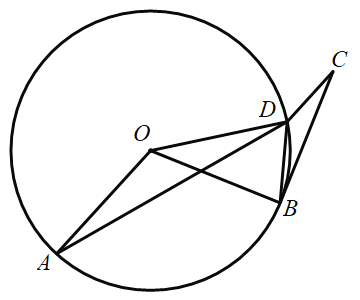
【题目】已知点![]() 是线段
是线段![]() 上与点
上与点![]() 不重合的一点,且
不重合的一点,且![]() 绕点
绕点![]() 逆时针旋转角
逆时针旋转角![]() 得到
得到![]() 绕点
绕点![]() 顺时针旋转角
顺时针旋转角![]() 得到
得到![]() ,连接
,连接![]()
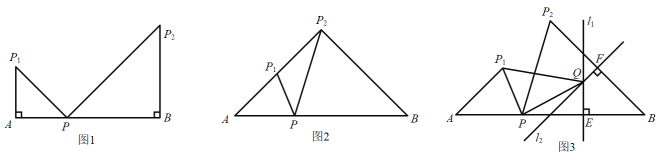
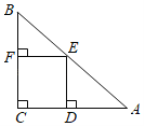
(1)如图1,当![]() 时,求
时,求![]() 的度数;
的度数;
(2)如图2,当点![]() 在
在![]() 的延长线上时,求证:
的延长线上时,求证: ![]() ;
;
(3)如图3,过![]() 的中点
的中点![]() 作
作![]() ,过
,过![]() 的中点
的中点![]() 作
作![]() ,
, ![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)利用旋转的性质以及等腰直角三角形得出∠APP1=∠BPP2=45°,进而得出答案;
(2)根据题意得出△PAP1和△PBP2均为顶角为α的等腰三角形,进而得出∠P1PP2=∠PAP2=α,求出△P2P1P∽△P2PA;
(3)首先连结QB,作![]() ,利用HL得出
,利用HL得出![]() ,利用角度的计算得出
,利用角度的计算得出![]() ,利用勾股定理求得PQ的长,再证明
,利用勾股定理求得PQ的长,再证明![]() ,求得PM的长,再利用勾股定理求出即可.
,求得PM的长,再利用勾股定理求出即可.
(1)解:由旋转的性质得:AP=AP1,BP=BP2.
∵α=90°,
∴△PAP1和△PBP2均为等腰直角三角形,
∴∠APP1=∠BPP2=45°,
∴∠P1PP2=180°-∠APP1-∠BPP2=90°;
(2)证明:由旋转的性质可知△PAP1和△PBP2均为顶角为α的等腰三角形,
∴∠APP1=∠BPP2=90°![]() ,
,
∴∠P1PP2=180°-(∠APP1+∠BPP2)=180°-2(90°![]() )=
)=![]() ,
,
在△P2P1P和△P2PA中,∠P1PP2=∠PAP2=α,
又∵∠PP2P1=∠AP2P,
∴△P2P1P∽△P2PA,
∴![]() ,
,
∴![]() ;
;
(3)证明:如图,连接QB,并过A作![]() ,垂足为M,
,垂足为M,
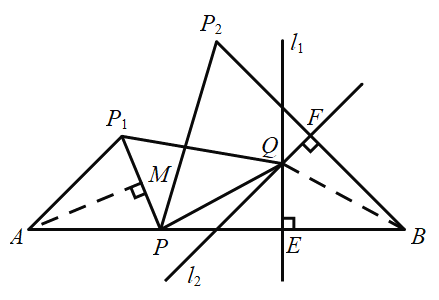
则![]() ,
,![]() ,
,
∵![]() 1,
1,![]() 2分别为PB,P2B的中垂线,
2分别为PB,P2B的中垂线,![]() ,
,
∴QP=QB,PE=BE=BF=![]() ,
,
又∵BQ=BQ,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
且AP=6,QE=1,
∴![]() ,
,![]() ,
,
∴![]() 中,
中,![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为![]() 分)、
分)、![]() 分)、
分)、![]() 分)、
分)、![]() 分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
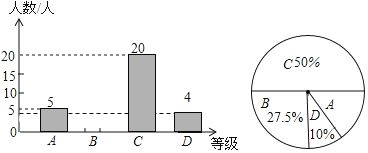
其中组![]() 的期末数学成绩如下
的期末数学成绩如下
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请补全条形统计图;
(2)这部分学生的期末数学成绩的中位数是 ,![]() 组的期末数学成绩的众数是 ;
组的期末数学成绩的众数是 ;
(3)这个学校九年级共有学生![]() 人,若分数为
人,若分数为![]() 分(含
分(含![]() 分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
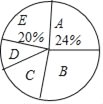
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?
【题目】某校为提高学生体考成绩,对全校300名九年级学生进行一分种跳绳训练.为了解学生训练效果,学校体育组在九年级上学期开学初和学期末分别对九年级学生进行一分种跳绳测试,学生成绩均为整数,满分20分,大于18分为优秀.现随机抽取了同一部分学生的两次成绩进行整理、描述和分析.(成绩得分用x表示,共分成五组:A.x<13,B.13≤x<15,C.15≤x<17,D.17≤x<19,E.19≤x≤20)
开学初抽取学生的成绩在D组中的数据是:17,17,17,17,17,18,18.
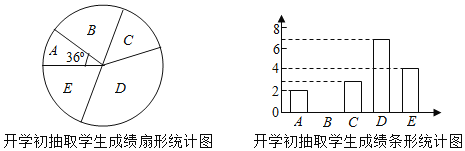
学期末抽取学生成绩统计表
学生成绩 | A组 | B组 | C组 | D组 | E组 |
人数 | 0 | 1 | 4 | 5 | a |
分析数据:
平均数 | 中位数 | 众数 | |
开学初抽取学生成绩 | 16 | b | 17 |
学期末抽取学生成绩 | 18 | 18.5 | 19 |
根据以上信息,解答下列问题:
(1)直接写出图表中a、b的值,并补全条形统计图;
(2)假设该校九年级学生都参加了两次测试,估计该校学期末成绩优秀的学生人数比开学初成绩优秀的学生人数增加了多少?
(3)小莉开学初测试成绩16分,学期末测试成绩19分,根据抽查的相关数据,请选择一个合适的统计量评价小莉的训练效果.