题目内容

9．某种商品每件的进价为30元，在某段时间内若以每件x元出售，可卖出（100-x）件，获利y元，当获利最大时，售价x=65元．

分析 本题是营销问题，基本等量关系：利润=每件利润×销售量，每件利润=每件售价-每件进价．再根据所列二次函数求最大值．

解答 解：设最大利润为w元，
则w=（x-30）（100-x）=-（x-65）2+1225，
∵-1＜0，0＜x＜100，
∴当x=65时，二次函数有最大值1225，
∴售价x=65元时，利润最大．
故答案为：65．

点评 本题考查了把实际问题转化为二次函数，再利用二次函数的性质进行实际应用．此题为数学建模题，借助二次函数解决实际问题．

练习册系列答案
相关题目
14．方程组$\left\{\begin{array}{l}{2x+y=5}\\{2x-y=-1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$．
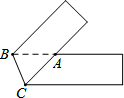15．将一张宽为5cm的长方形纸片（足够长）折叠成如图所示图形，重叠部分是一个三角形，则这个三角形面积的最小值是$\frac{25}{2}$cm2．
12．如图①，△ABC与△CDE是等腰直角三角形，直角边AC、CD在同一条直线上，点M、N分别是斜边AB、DE的中点，点P为AD的中点，连接AE、BD．
（1）猜想PM与PN的数量关系及位置关系，请直接写出结论；
（2）现将图①中的△CDE绕着点C顺时针旋转α（0°＜α＜90°），得到图②，AE与MP、BD分别交于点G、H．请判断（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由；
（3）若图②中的等腰直角三角形变成直角三角形，使BC=kAC，CD=kCE，如图③，写出PM与PN的数量关系，并加以证明．
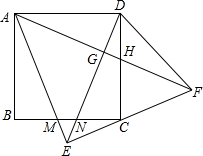4．如图，正方形ABCD中，以AD为底边作等腰△ADE，将△ADE沿DE折叠，点A落到点F处，连接EF刚好经过点C，再连接AF，分别交DE于G，交CD于H．在下列结论中：
①△ABM≌△DCN；②∠DAF=30°；③△AEF是等腰直角三角形；④EC=CF；⑤S△HCF=S△ADH，
其中正确的结论有（　　）
A．2个B．3个C．4个D．5个
14．已知a、b、c是三角形的三边，且满足|a-$\frac{3}{2}$|+（b-2）2+$\sqrt{c-\frac{5}{2}}$=0，则这个三角形是（　　）
A．等腰三角形B．直角三角形C．等腰直角三角形D．钝角三角形
1．某旅游景点的收入受季节的影响较大，有时候出现赔本的经营状况．因此，公司规定：若无利润时，该景点关闭．经跟踪测算，该景点一年中的利润W（万元）与月份x之间满足二次函数W=-x2+16x-48，则该景点一年中处于关闭状态有（　　）月．
A．5B．6C．7D．8
18．综合与实践：制作礼品盒
如图（1），小颖将边长为60cm的正方形硬纸片ABCD，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，如图（2），点A，B，C，D四点重合于点P，做成一个底面是正方形的长方体形状的礼品盒．设礼品盒的侧面积为Scm2，AE=FB=xcm．

（1）求S与x之间的关系式及S的最大值；
（2）小颖有一底面半径为15cm，高为15cm的圆柱体形状的礼品，该礼品能否底面朝下放入她做成的礼品盒？若能，求出x的值；若不能，请说明理由．
19．小滨初中就要毕业了，她就本班同学的升学志愿进行了一次调查统计，她通过采集数据绘制了两幅不完整的统计图，请你根据图中提供的信息，解答下列问题：
（1）求出该班的总人数；
（2）通过计算请把条形统计图补充完整；
（3）如果小滨所在年级共有760名学生，请你估计该年级报考普高的学生人数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网