题目内容
20.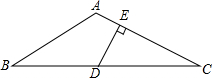 如图,△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于E,AE=1,求CE的长.
如图,△ABC中,AB=AC,∠BAC=120°,D为BC的中点,DE⊥AC于E,AE=1,求CE的长.
分析 连接AD,根据三线合一得到AD垂直于BC,AD为角平分线,以及底角的度数,在直角三角形ADE中,利用30角所对的直角边等于斜边的一半得到AD的长,在直角三角形ADE中,再利用30角所对的直角边等于斜边的一半求出AC的长,由AC-AE即可求出CE的长.
解答 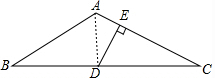 解:连接AD,
解:连接AD,
∵AB=AC,∠BAC=120°,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,∠B=∠C=30°
∴∠DAC=$\frac{1}{2}$∠BAC=60°,
∵DE⊥AC于E,
∴∠AED=90°,
∴∠ADE=30°,
在Rt△ADE中,AE=1,∠ADE=30°,
∴AD=2AE=2,
在Rt△ADC中,AD=2,∠C=30°,
∴AC=2AD=4,
则CE=AC-AE=4-1=3.
点评 此题考查了含30度直角三角形的性质,等腰三角形的性质,以及三线合一,熟练掌握性质是解本题的关键.

练习册系列答案
相关题目
11.-2的绝对值是( )
| A. | $\frac{1}{2}$ | B. | ±2 | C. | 2 | D. | -2 |
10.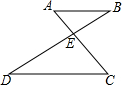 如图,已知AB∥CD,AC、BD相交于点E,AB=2,CD=5,则△ABE与△CDE的周长之比是( )
如图,已知AB∥CD,AC、BD相交于点E,AB=2,CD=5,则△ABE与△CDE的周长之比是( )
 如图,已知AB∥CD,AC、BD相交于点E,AB=2,CD=5,则△ABE与△CDE的周长之比是( )
如图,已知AB∥CD,AC、BD相交于点E,AB=2,CD=5,则△ABE与△CDE的周长之比是( )| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{25}$ | D. | $\frac{8}{125}$ |
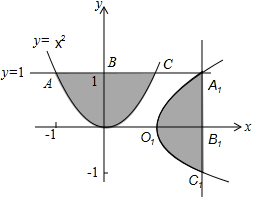 如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1.
如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1.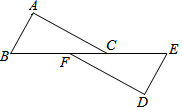 如图,△ABC≌△DEF,则下列结论中,成立的有①②③④.(填序号)
如图,△ABC≌△DEF,则下列结论中,成立的有①②③④.(填序号)