题目内容
19.已知一次函数y=-2x+3,填空:(1)k=-2,b=3;
(2)当x=0时,y=3;当x=$\frac{3}{2}$时,y=0;
(3)当x=3时,y=-3;当y=3时,x=0.
分析 (1)根据函数解析式即可求解;
(2)把x=0,y=0分别代入求得即可;
(3)把x=3,y=3分别代入即可求得.
解答 解:(1)∵一次函数y=-2x+3,
∴k=-2,b=3;
(2)当x=0时,y=3;
当y=0时,则-2x+3=0,
∴x=$\frac{3}{2}$;
(3)当x=3时,y=-2×3+3=-3;
当y=3时,则-2x+3=3,
∴x=0.
故答案为:-2,3;3,$\frac{3}{2}$;-3,0.
点评 本题考查一次函数图象上点的坐标特征,图象上的点的坐标适合解析式.

练习册系列答案
相关题目
14.若式子$\frac{1-x}{2}$与1-$\frac{x+1}{3}$的值相等,则x=( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
11.-2的绝对值是( )
| A. | $\frac{1}{2}$ | B. | ±2 | C. | 2 | D. | -2 |
 如图,△ABC中,边AB的中垂线分别交BC、AB于点D、E,AE=3cm,△ABC的周长为18cm,则△ADC的周长是12 cm.
如图,△ABC中,边AB的中垂线分别交BC、AB于点D、E,AE=3cm,△ABC的周长为18cm,则△ADC的周长是12 cm.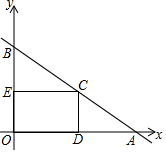 如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(6,0),B(0,3)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.
如图,平面直角坐标系中,直线AB与x轴,y轴分别交于A(6,0),B(0,3)两点,点C为线段AB上的一动点,过点C作CD⊥x轴于点D.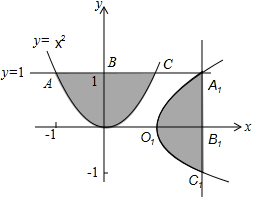 如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1.
如图,把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后,再沿x轴向右平移1个单位得到图形O1A1B1C1.