题目内容
2.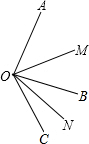 如图,已知∠AOB=80°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.
如图,已知∠AOB=80°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.(1)求∠MON的度数;
(2)若(1)中∠AOB=α,其他条件不变,求∠MON的大小;
(3)若(1)中∠BOC=β,(β为锐角),其他条件不变,求∠MON的大小;
(4)从(1)(2)(3)的结果中,能看出什么规律?
分析 (1)根据角平分线的定义进行解答,求出∠MON的度数;
(2)与(1)的解题思路相同,求出∠MON的度数;
(3)根据角平分线的定义和图形,求出∠MON的度数;
(4)根据以上计算结果,总结规律即可.
解答 解:∵∠AOC=∠AOB+∠BOC,
∴∠AOC=120°,
∵OM平分∠AOC,
∴∠MOC=60°,
∵ON平分∠BOC,
∴∠NOC=20°,
∴∠MON=60°-20°=40°;
(2)同理可知,∠MOC=$\frac{1}{2}$(α+40°),∠NOC=20°,
∴∠MON=$\frac{1}{2}α$;
(3)同理可知,∠MOC=$\frac{1}{2}$(80°+β),∠NOC=$\frac{1}{2}β$,
∠MON=40°;
(4)规律:∠MON=$\frac{1}{2}$∠AOB.
点评 本题考查的是角的有关计算和角平分线的定义,正确理解并灵活运用角平分线的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9. 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③$\widehat{BD}$=$\widehat{AD}$;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③$\widehat{BD}$=$\widehat{AD}$;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
 如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③$\widehat{BD}$=$\widehat{AD}$;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③$\widehat{BD}$=$\widehat{AD}$;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )| A. | ①② | B. | ①②③ | C. | ①④ | D. | ①②④ |
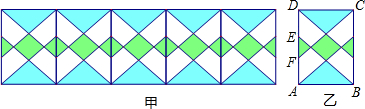
13.用火柴棒按下列方式搭建三角形:

(1)填表:
(2)当三角形的个数为n时,火柴棒的根数是多少?(用含n的式子表示)
(3)求当n=100时,火柴棒的根数是多少?
(4)当火柴棒的根数为2013时,三角形的个数是多少?

(1)填表:
| 三角形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 |
(3)求当n=100时,火柴棒的根数是多少?
(4)当火柴棒的根数为2013时,三角形的个数是多少?
10.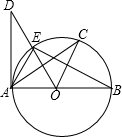 如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )
如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )
 如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )
如图,AB是⊙O的直径,AD切⊙O于点A,$\widehat{EC}$=$\widehat{CB}$.则下列结论:①BA⊥DA;②OC∥AE;③∠COE=2∠CAE;④OD⊥AC,一定正确的个数有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
 如图,?OABC的顶点C在x轴的正半轴上,顶点A、B在第一象限内,且点A的横坐标为2,对角线AC与OB交于点D,若反比例函数y=$\frac{10}{x}$的图象经过点A与点D,则?OABC的面积为( )
如图,?OABC的顶点C在x轴的正半轴上,顶点A、B在第一象限内,且点A的横坐标为2,对角线AC与OB交于点D,若反比例函数y=$\frac{10}{x}$的图象经过点A与点D,则?OABC的面积为( )