题目内容
18.根据下列要求,解答相关问题.(1)请补全以下求不等式-2x2-4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=-2x2-4x;并在下面的坐标系中(图1)画出二次函数y=-2x2-4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程-2x2-4x=0的解为x1=0,x2=-2;并用锯齿线标示出函数y=-2x2-4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式-2x2-4x>0的解集为-2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2-2x+1≥4的解集.
分析 ①利用描点法即可作出函数的图象;
②当y=0时,解方程求得x的值,当y>0时,就是函数图象在x轴上方的部分,据此即可解得;
③仿照上边的例子,首先作出函数y=x2-2x+1的图象,然后求得当y=4时对应的x的值,根据图象即可求解.
解答 解:①图所示: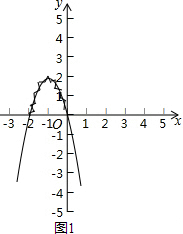 ;
;
②方程-2x2-4x=0即-2x(x+2)=0,
解得:x1=0,x2=-2;
则方程的解是x1=0,x2=-2,
图象如图1;
③函数y=x2-2x+1的图象是: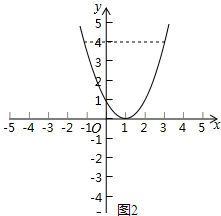
当y=4时,x2-2x+1=4,解得:x1=3,x2=-1.
则不等式的解集是:x≥3或x≤-1.
点评 本题考查了二次函数与不等式的关系,理解函数的图象在x轴上方,则函数值大于0是本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
8.将二次函数y=-2(x-1)2-2的图象向左平移1个单位,则其顶点为( )
| A. | (0,0) | B. | (1,-2) | C. | (0,-2) | D. | (-2,1) |
6.若x+m与x+3的乘积中不含x的一次项,则m的值为( )
| A. | 0 | B. | 1 | C. | 3 | D. | -3 |
3.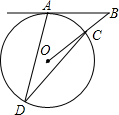 如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )
如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )
 如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )
如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
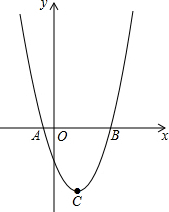 已知抛物线的顶点坐标C(4,-9),且过点(-1,16).
已知抛物线的顶点坐标C(4,-9),且过点(-1,16). 如图,D是AB边上的中点,将△ABC的沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠ADE=50度.
如图,D是AB边上的中点,将△ABC的沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠ADE=50度.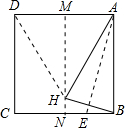 如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下得到△ADH,则下列选项正确的个数为( )
如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下得到△ADH,则下列选项正确的个数为( )