题目内容
9.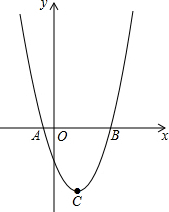 已知抛物线的顶点坐标C(4,-9),且过点(-1,16).
已知抛物线的顶点坐标C(4,-9),且过点(-1,16).(1)求抛物线的解析式.
(2)若函数图象与x轴交于A,B两点,求△ABC的面积.
分析 (1)设该抛物线方程为y=a(x-4)2-9,然后将点(-1,16)代入即可求得a的值;
(2)令y=0,求出抛物线与x轴的交点坐标,然后根据三角形的面积公式列式进行计算即可求解.
解答 解:(1)∵抛物线的顶点坐标为C(4,-9),
∴设该抛物线方程为y=a(x-4)2-9,
又∵它的图象经过点(-1,16),
∴16=a(-1-4)2-9,
解得:a=1,
∴该抛物线的解析式为y=(x-4)2-9=x2-8x+7;
(2)令y=0,则x2-8x+7=0,
解得x1=1,x2=7,
则A点坐标为,B两点
△ABC的面积=$\frac{1}{2}$×(7-1)×9=27.
点评 本题考查了抛物线与x轴的交点坐标,待定系数法求二次函数解析式,利用顶点式解析式求得函数解析式是解题的关键.

练习册系列答案
相关题目
1.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
19.下列各式中互为相反数的算式是( )
①-(-3)②(-3)2 ③|-(-3)|④-|-32|
①-(-3)②(-3)2 ③|-(-3)|④-|-32|
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
 如图所示的阴影部分面积用代数式表示为ab-$\frac{1}{2}π{b}^{2}$.
如图所示的阴影部分面积用代数式表示为ab-$\frac{1}{2}π{b}^{2}$. 已知一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)
已知一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)