Question

12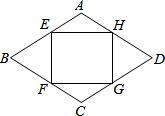．如图，在菱形ABCD的边上依次取点E，F，G，H，使AE=AH=CF=CG，若菱长边长是1，∠A=120°，
（1）求证：四边形EFGH是矩形；
（2）设AE=x，四边形EFGH的面积是y，求y与x的函数关系式；
（3）当x为何值时，四边形EFGH是正方形？

Answer 1

分析 （1）首先利用菱形的性质得到∠A=∠C，∠B=∠D，AB=BC=CD=DA，然后根据AE=AH=CF=CG，得到BE=BF=DH=DG，从而证得△AEH≌△CGF，△BEF≌△DGH，证得四边形EFGH是平行四边形，然后利用有一个角是直角的平行四边形是矩形判定四边形EFGH是矩形；
（2）先求出AC=1，再求出BE=1-x，再用三角函数得出PE=$\frac{\sqrt{3}}{2}$x进而得出EH=$\sqrt{3}$x，最后用矩形的面积公式即可得出结论；
（3）由（2）EH=$\sqrt{3}$x，EF=1-x，再用正方形的性质即可建立方程求出x值即可．

解答 （1）证明：∵四边形ABCD是菱形，
∴∠A=∠C，∠B=∠D，AB=BC=CD=DA
∵AE=AH=CF=CG，
∴BE=BF=DH=DG，
∴△AEH≌△CGF，△BEF≌△DGH，
∴EH=FG，EF=GH，
∴四边形EFGH是平行四边形，
∵∠A+∠D=180°，
∴∠AHE+∠DHG=90°，
∴∠EHG=90°，
∴四边形EFGH是矩形；

（2）解：如图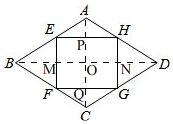，连接AC，交EH，FG于P，Q，连接BD交EF，HG于M，N，
∵四边形ABCD是菱形，∠BAC=120°，
∴∠ABC=60°，
∴AC=AB=1，
由（1）知，四边形EFGH是矩形，
∴EF∥AC，
∴EF=BE=AB-AE=1-x，
在Rt△APE中，∠PAE=$\frac{1}{2}$∠BAD=60°，
∴sin∠PAE=$\frac{PE}{AE}$，
∴PE=AEsin∠PAE=x•sin60°=$\frac{\sqrt{3}}{2}$x，
∴EH=2PE=$\sqrt{3}$x，
∴四边形EFGH的面积是y=EF•EH=（1-x）•$\sqrt{3}$x=-$\sqrt{3}$x²+$\sqrt{3}$x，（0＜x＜1）；

（3）解：由（2）知，EH=$\sqrt{3}$x，EF=1-x，
∵矩形EFGH是正方形，
∴EF=EH，
∴$\sqrt{3}$x=1-x，
∴x=$\frac{\sqrt{3}-1}{2}$．

点评 此题是四边形综合题，主要考查了全等三角形的判定和性质，菱形的性质，等边三角形的判定和性质，矩形的判定，正方形的性质，解（1）的关键先判断四边形EFGH是平行四边形，解（2）的关键是用x表示EF和
EH，解（3）的关键是掌握正方形的性质，是一道中等难度的题目．