题目内容
 如图,已知AB是⊙O的直径,△ABC内接于⊙O,BD平分△ABC的外角∠ABF交⊙O于点D,DE⊥BC于点E.
如图,已知AB是⊙O的直径,△ABC内接于⊙O,BD平分△ABC的外角∠ABF交⊙O于点D,DE⊥BC于点E.(1)判断DE和⊙O的位置关系,并说明理由;
(2)若∠A=30°,AB=4cm,求DE的长.
考点:切线的判定,等边三角形的判定与性质,勾股定理
专题:计算题
分析:(1)DE与圆O相切,理由为:连接OD,由BD为角平分线,得到一对角相等,再由OB=OD,利用等边对等角得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到OD与CE平行,而CE与DE垂直,可得出OD与DE垂直,即可确定出DE为圆O的切线;
(2)由AB为圆O的直径,利用直径所对的圆周角为直角得到∠C为直角,再由∠A的度数,求出∠ABC的度数,利用两直线平行内错角相等求出∠BOD为60°,确定出三角形OBD为等边三角形,求出∠BDO为60°,得到∠BDE为30°,在直角三角形BDE中,由BD=2cm,利用锐角三角函数定义及特殊角的三角函数值即可求出DE的长.
(2)由AB为圆O的直径,利用直径所对的圆周角为直角得到∠C为直角,再由∠A的度数,求出∠ABC的度数,利用两直线平行内错角相等求出∠BOD为60°,确定出三角形OBD为等边三角形,求出∠BDO为60°,得到∠BDE为30°,在直角三角形BDE中,由BD=2cm,利用锐角三角函数定义及特殊角的三角函数值即可求出DE的长.
解答: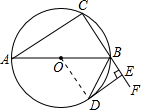 解:(1)DE与圆O相切,理由为:
解:(1)DE与圆O相切,理由为:
证明:连接OD,
∵BD平分∠ABF,
∴∠OBD=∠DBE,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠DBE=∠ODB,
∴OD∥CE,又CE⊥DE,
∴OD⊥DE,
则DE为圆O的切线;
(2)∵AB为圆O的直径,
∴∠C=90°,
又∠A=30°,
∴∠ABC=60°,
∵OD∥CE,
∴∠BOD=∠ABC=60°,
∵OB=OD,
∴△OBD为等边三角形,即OB=OD=BD=2cm,
∴∠ODB=60°,∠BDE=30°,
在Rt△BDE中,BD=2cm,∠BDE=30°,
则DE=BDcos30°=2×
=
.
 解:(1)DE与圆O相切,理由为:
解:(1)DE与圆O相切,理由为:证明:连接OD,
∵BD平分∠ABF,
∴∠OBD=∠DBE,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠DBE=∠ODB,
∴OD∥CE,又CE⊥DE,
∴OD⊥DE,
则DE为圆O的切线;
(2)∵AB为圆O的直径,
∴∠C=90°,
又∠A=30°,
∴∠ABC=60°,
∵OD∥CE,
∴∠BOD=∠ABC=60°,
∵OB=OD,
∴△OBD为等边三角形,即OB=OD=BD=2cm,
∴∠ODB=60°,∠BDE=30°,
在Rt△BDE中,BD=2cm,∠BDE=30°,
则DE=BDcos30°=2×
| ||
| 2 |
| 3 |
点评:此题考查了切线的判定,等边三角形的判定与性质,勾股定理,圆周角定理,特殊角的三角函数值,以及锐角三角函数定义,其中切线的判定方法有两种:有点连接证明垂直;无点连接证明垂线段等于圆的半径.

练习册系列答案
相关题目
在△ABC中,∠B=∠C=75°,AB=2,则△ABC的面积是( )
| A、2 | B、1 | C、1.5 | D、0.5 |
同时投掷两颗骰子,则两个点数不同的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 初三某班一女生在一次投掷实心球的测试中,实心球所经过的路线为如图所示的抛物线y=-
初三某班一女生在一次投掷实心球的测试中,实心球所经过的路线为如图所示的抛物线y=-| 1 |
| 9 |
| 2 |
| 3 |
| 16 |
| 9 |
A、实心球的出手高度为
| ||
| B、实心球飞出2米后达到最大高度 | ||
| C、实心球在飞行过程中的最大高度为3米 | ||
| D、该同学的成绩是8米 |
 如图,AB∥CD,AC与BD交于点E,若BE:BD=1:3,则△ABE与△DCE的面积比为
如图,AB∥CD,AC与BD交于点E,若BE:BD=1:3,则△ABE与△DCE的面积比为 如图所示,AE⊥AB,且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6,3,2,则图中实线所围成的阴影部分面积S是( )
如图所示,AE⊥AB,且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6,3,2,则图中实线所围成的阴影部分面积S是( )