题目内容
6.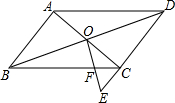 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,AB=2,BC=3,CE=1,则CF=$\frac{3}{4}$.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,AB=2,BC=3,CE=1,则CF=$\frac{3}{4}$.
分析 过O作OM∥BC交CD于M,根据平行四边形的性质得到BO=DO,CD=AB=4,AD=BC=6,根据三角形的中位线的性质得到CM=$\frac{1}{2}$CD=2,OM=$\frac{1}{2}$BC=3,通过△CFE∽△EMO,根据相似三角形的性质得到$\frac{CF}{OM}$=$\frac{CE}{EM}$,代入数据即可得到结论.
解答 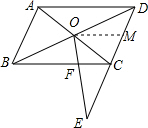 解:过O作OM∥BC交CD于M,
解:过O作OM∥BC交CD于M,
∵在?ABCD中,BO=DO,CD=AB=2,AD=BC=3,
∴CM=$\frac{1}{2}$CD=1,OM=$\frac{1}{2}$BC=$\frac{3}{2}$,
∵OM∥CF,
∴△CFE∽△EMO,
∴$\frac{CF}{OM}$=$\frac{CE}{EM}$,
即$\frac{CF}{\frac{3}{2}}$=$\frac{1}{2}$,
∴CF=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 此题考查了平行四边形的性质、相似三角形的判定与性质等知识.解此题的关键是准确作出辅助线,合理应用数形结合思想解题.

练习册系列答案
相关题目
18.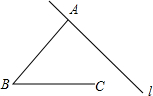 如图所示的平面图形中,下列说法错误的是( )
如图所示的平面图形中,下列说法错误的是( )
 如图所示的平面图形中,下列说法错误的是( )
如图所示的平面图形中,下列说法错误的是( )| A. | 直线l经过点A | B. | 射线BC不与直线l相交 | ||
| C. | 点B在直线l外 | D. | 点A到点B的距离是线段AB的长度 |

 如图,将一根长为20cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,筷子露在杯子外面的长度为7cm.
如图,将一根长为20cm的筷子置于底面直径为5cm,高为12cm的圆柱形水杯中,筷子露在杯子外面的长度为7cm. 如图,已知,线段AB=6,点C是AB的中点,点D是线段AC上的点,且DC=$\frac{1}{3}$AC,求线段BD的长.
如图,已知,线段AB=6,点C是AB的中点,点D是线段AC上的点,且DC=$\frac{1}{3}$AC,求线段BD的长.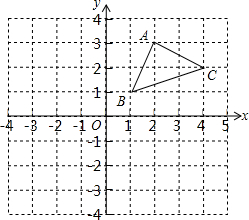 如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2).
如图,在平面直角坐标系中有三个点A(2,3),B(1,1),C(4,2). 已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C.
已知抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C.