题目内容
2.实数a、b、c、d满足:一元二次方程x2+cx+d=0的两根为a、b,一元二次方程x2+ax+b=0的两根为c、d,则所有满足条件的数组(a、b、c、d)为(1,-2,1,-2)或(a,0,-a,0)(a为任意实数).分析 根据根与系数的关系可以得到a、b、c、d之间的关系,联立方程组即可求得它们之间的关系,本题得以解决.
解答 解:∵实数a、b、c、d满足:一元二次方程x2+cx+d=0的两根为a、b,一元二次方程x2+ax+b=0的两根为c、d,
∴$\left\{\begin{array}{l}{a+b=-c}\\{ab=d}\\{c+d=-a}\\{cd=b}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\\{c=1}\\{d=-2}\end{array}\right.$或$\left\{\begin{array}{l}{a=-c}\\{b=d=0}\end{array}\right.$(a为任意实数).
故答案为:(1,-2,1,-2)或(a,0,-a,0)(a为任意实数).
点评 本题考查根与系数的关系,解题的关键是明确根与系数的关系是什么.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
20.已知:当x=2时,多项式x4-bx2+c的值为2016,当x=-2时,多项式x4-bx2+c的值为( )
| A. | -2016 | B. | -2015 | C. | 2016 | D. | 2015 |
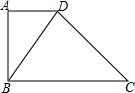 如图,已知四边形ABCD中,∠A=90°,AD∥BC.
如图,已知四边形ABCD中,∠A=90°,AD∥BC. 圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A=40°.
圆内接四边形ABCD,两组对边的延长线分别相交于点E、F,且∠E=40°,∠F=60°,求∠A=40°.