题目内容

2．在△ABC中，D是AB的中点，DE∥BC，则S△ADE：S△ABC=1：4．

分析 由平行可知△ADE∽△ABC，根据D是AB的中点，可得$\frac{AD}{AB}$=$\frac{1}{2}$，再利用三角形的面积比等于相似比的平方，可求得比值．

解答 解：∵DE∥BC，
∴△ADE∽△ABC，
∵D是AB的中点，
∴$\frac{AD}{AB}$=$\frac{1}{2}$，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{AD}{AB}$）2=$\frac{1}{4}$．
故答案为：1：4．

点评 本题主要考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．

练习册系列答案
相关题目
12．单项式-$\frac{1}{3}$πa2b3的系数是-$\frac{1}{3}$π．
13．关于x的分式方程$\frac{7}{x-1}$+3=$\frac{m}{x-1}$无解，m的值为（　　）
A．7B．-7C．1D．-1
10．如图，C是线段AB的中点，D、E分别是线段AC，CB上的点，且AD=$\frac{2}{3}$AC，DE=$\frac{3}{5}$AB，若AB=24cm，求线段CE的长．
17．对于任意非零有理数a，b定于运算如下：a*b=（a-b）÷（a+b），则（-3）*5的值为-4．
7．半径为2的圆内接正六边形的边心距是$\sqrt{3}$．
14．已知不等式2x-a＜0的正整数解只有两个，则a的取值范围是4＜a≤6．
11．把下列各数分别填入相应的打括号内：
-5，10，-4$\frac{1}{2}$，0，+2$\frac{1}{2}$，-2.15，0.01，+66，15%，$\frac{3}{102}$，2016，-16
自然数集合{10，0，+66，2016}；
整数集合{-5，10，0，+66，2016，-16}；
正分数集合{2$\frac{1}{2}$，0.01，15%，$\frac{3}{102}$}；
非正数集合{-5，-4$\frac{1}{2}$，0，-2.15，-16}；
有理数集合{-5，10，-4$\frac{1}{2}$，0，+2$\frac{1}{2}$，-2.15，0.01，+66，15%，$\frac{3}{102}$，2016，-16}．
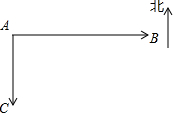20．如图，甲船以15千米/小时的速度从港口A向正南方向航行，同时乙船以20千米/小时的速度从港口B向港口A方向航行．已知港口B在港口A的正东方向，且相距80千米．则行驶2小时后两船相距50千米．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网